Question

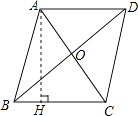
【题目】如图，在ABCD中，对角线AC，BD相交于点O，AB=5，AC=6，BD=8．
（1）求证：四边形ABCD是菱形；
（2）过点A作AH⊥BC于点H，求AH的长．

Answer 1

【答案】
（1）证明：∵在ABCD中，对角线AC，BD相交于点O，AB=5，AC=6，BD=8，

∴AO= AC=3，BO= BD=4，

∵AB=5，且32+42=52，

∴AO2+BO2=AB2，

∴△AOB是直角三角形，且∠AOB=90°，

∴AC⊥BD，

∴四边形ABCD是菱形

（2）解：如图所示：

∵四边形ABCD是菱形，

∴BC=AB=5，

∵S△ABC= ACBO= BCAH，

∴ ×6×4= ×5×AH，

解得：AH= ．

【解析】（1）利用平行四边形的性质结合勾股定理的逆定理得出△AOB是直角三角形，进而得出四边形ABCD是菱形；（2）利用菱形的面积求法得出AH的长．