题目内容
解不等式组,并把它的解集在数轴上表示出来(1)9-4(x-5)<7x+4;
(2)
| x |
| 2 |
| 0.1x+0.8 |
| 0.6 |
| x+1 |
| 3 |
(3)
|
(4)
|
分析:(1)(2)根据一元一次不等式的解法思路有移项、化简(同乘除)可求得.(3)(4)根据求一元一次不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解)可求得.
解答:解:(1)9-4(x-5)<7x+4
去括号得:9-4x+20<7x+4,
移项合并得:11x>25,
化系数为1得:x>
.
在数轴上表示得:
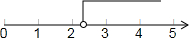
(2)
-
<1-
化简得:
-
<1-
,
去分母得:3x-(x+8)<6-2(x+1),
去括号得:3x-x-8<6-2x-2,
移项合并得:4x<12,
化系数为1得:x<3.
在数轴上表示得:

(3)
解:解不等式①得:x>
,
解不等式②得:x≤4,
∴不等式组的解集
<x≤4.
在数轴上表示得:
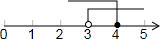
(4)
解:解不等式①得:x≥-
,
解不等式②得:x>1,
∴不等式组的解集为x>1,
在数轴上表示得:
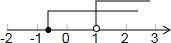
去括号得:9-4x+20<7x+4,
移项合并得:11x>25,
化系数为1得:x>
| 25 |
| 11 |
在数轴上表示得:

(2)
| x |
| 2 |
| 0.1x+0.8 |
| 0.6 |
| x+1 |
| 3 |
化简得:
| x |
| 2 |
| x+8 |
| 6 |
| x+1 |
| 3 |
去分母得:3x-(x+8)<6-2(x+1),
去括号得:3x-x-8<6-2x-2,
移项合并得:4x<12,
化系数为1得:x<3.
在数轴上表示得:

(3)
|
解:解不等式①得:x>
| 5 |
| 2 |
解不等式②得:x≤4,
∴不等式组的解集
| 5 |
| 2 |
在数轴上表示得:

(4)
|
解:解不等式①得:x≥-
| 2 |
| 3 |
解不等式②得:x>1,
∴不等式组的解集为x>1,
在数轴上表示得:

点评:本题考查一元一次不等式、一元一次不等式组的解法:一元一次不等式的解法思路有移项、化简(同乘除).求一元一次不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).

练习册系列答案
相关题目