题目内容
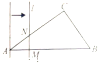
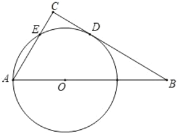
【题目】如图,已知![]() 中,
中,![]() ,点
,点![]() 为斜边
为斜边![]() 上一点,且
上一点,且![]() ,以
,以![]() 为半径的
为半径的![]() 与
与![]() 相切于
相切于![]() ,与
,与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
(1)求线段![]() 的长;
的长;
(2)求![]() 与
与![]() 重叠部分的面积.(结果保留准确值)
重叠部分的面积.(结果保留准确值)
【答案】(1)![]() ;(2)
;(2)![]() ;
;
【解析】
(1)连接OD,由切线的性质和直角三角形的性质得出OB=2OD=4,BD=![]() OD=
OD=![]() ,得出AB=OA+OB=6,AC=
,得出AB=OA+OB=6,AC=![]() AB=3,BC=
AB=3,BC=![]() AC=
AC=![]() ,即可得出结果;
,即可得出结果;
(2)连接OE,证出△OAE是等边三角形,得出∠AOE=60°,∠EOG=120°,作EF⊥OA于F,则OF=1,EF=![]() OF=
OF=![]() ,⊙O与Rt△ABC重叠部分的面积=△AOE的面积+扇形OEDG的面积,即可得出结果.
,⊙O与Rt△ABC重叠部分的面积=△AOE的面积+扇形OEDG的面积,即可得出结果.
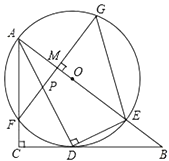
解:(1)连接OD,如图1所示:
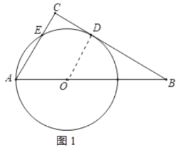
∵以OA为半径的⊙O与BC相切于D,
∴∠ODB=90°,
∵OD=OA=2,∠C=90°,∠CAB=60°,
∴∠B=30°,
∴OB=2OD=4,BD=![]() OD=
OD=![]() ,
,
∴AB=OA+OB=6,
∴AC=![]() AB=3,
AB=3,
∴BC=![]() AC=
AC=![]() ,
,
∴CD=BCBD=![]() ;
;
(2)连接OE,如图2所示:
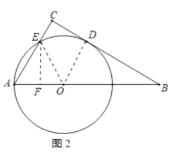
则OA=OE,
∵∠CAB=60°,
∴△OAE是等边三角形,
∴∠AOE=60°,
∴∠EOG=120°,
作EF⊥OA于F,
则OF=1,EF=![]() OF=
OF=![]() ,
,
∴⊙O与Rt△ABC重叠部分的面积=△AOE的面积+扇形OEDG的面积=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目