Question

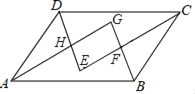
【题目】如图，在ABCD中，各内角的平分线相交于点E，F，G，H．

（1）求证：四边形EFGH是矩形；

（2）若AB=6，BC=4，∠DAB=60°，求四边形EFGH的面积．

Answer 1

【答案】（1）证明见解析；（2）矩形EFGH的面积= ．

【解析】

（1）根据角平分线的定义以及平行四边形的性质，即可得出∠AGB=90°，∠DEC=90°，∠AHD=90°=∠EHG，进而判定四边形EFGH是矩形；

（2）根据含30°角的直角三角形的性质，得到BGAB=3，AG=3CE，BFBC=2，CF=2，进而得出EF和GF的长，可得四边形EFGH的面积．

（1）∵GA平分∠BAD，GB平分∠ABC，∴∠GAB∠BAD，∠GBA∠ABC．

∵ABCD中，∠DAB+∠ABC=180°，∴∠GAB+∠GBA（∠DAB+∠ABC）=90°，即∠AGB=90°，同理可得：∠DEC=90°，∠AHD=90°=∠EHG，∴四边形EFGH是矩形；

（2）依题意得：∠BAG∠BAD=30°．

∵AB=6，∴BGAB=3，AG=3CE．

∵BC=4，∠BCF∠BCD=30°，∴BFBC=2，CF=2，∴EF=3，GF=3﹣2=1，∴矩形EFGH的面积=EF×GF．