Question

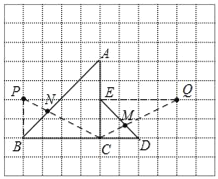
【题目】在每个小正方形的边长为1的网格中，等腰直角三角形与的顶点都在网格点上，点、分别为线段、上的动点，且．

（Ⅰ）如图①，当时，计算的值等于__；

（Ⅱ）当取得最小值时，请在如图②所示的网格中，用无刻度的直尺，画出线段和，并简要说明点和点的位置是如何找到的（不要求证明）．

Answer 1

【答案】 如图所示，取格点、，使得，，，，连接交于，连接交于，则线段和即为所求．

【解析】

（1）根据当时，点N和点M在格点上，运用勾股定理进行计算即可得到CN+CM的值；

（2）取格点P、Q，使得PB=CE，PB⊥BC，QE=CB，QE⊥AC，连接CP交AB于N，连接CQ交DE于M，则根据全等三角形的对应边相等，以及两点之间线段最短，可得线段CN和CM即为所求．

（1）当时，点和点在格点上，

，

故答案为：；

（2）如图所示，取格点、，使得，，，，

连接交于，连接交于，则线段和即为所求．

理由如下：

∵等腰直角三角形与的顶点都在网格点上，

∴，，

∵，

∴，，

，，

当，，三点共线时，（最短），

当，，三点共线时，（最短），

点和点的位置符合题意．