题目内容
已知Rt△ABC中,直角边AC=3,BC=4,P、Q分别是AB、BC上的动点,且点P不与A、B重合.点Q不与B、C重合.
(1)若CP⊥AB于点P,如图1,△CPQ为等腰三角形,这时满足条件的点Q有几个?直接写出相等的腰和相应的CQ的长(不写解答过程)
(2)当P是AB的中点时,如图2,若△CPQ与△ABC相似,这时满足条件的点Q有几个?分别求出相应的CQ的长?
(3)当CQ的长取不同的值时,除PQ垂直于BC的△CPQ外,其余的△CPQ是否可能为直角三角形?若可能,请说明所有情况?若不可能,请说明理由.
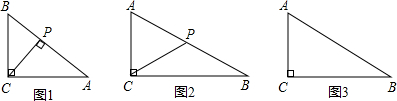
解:(1)当CP为等腰三角形的底边时作CP的垂直平分线,交BC于Q,
则腰是CQ=PQ;
此时CQ= BC=1.5;
BC=1.5;
当CP为腰时,在BC上截取CQ=CP,
则腰是CP=CQ′,
此时CQ=CP= =2.4;
=2.4;
(2)当P是AB的中点时,如图2,若△CPQ与△ABC相似,这时满足条件的点Q有3个,
①当△COQ∽△BCA,时,
∴ =
= ,
,
∴CQ= BC=2;
BC=2;
②△PQ′B∽△CAB时,
∴ ,
,
∵AP=BP= AB=2.5,BC=4,
AB=2.5,BC=4,
∴ ,
,
∴BQ′= ,
,
∴CQ′=4- =
= ;
;
③△CPQ″∽△BCA时,
∴ ,
,
∴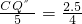 ,
,
∴CQ″= ;
;
(3)可能.
过Q作QP⊥BC,交AB于P点,连接CP,则△CPQ为直角三角形,作∠CAB的平分线AO,交BC于O点.作OP1⊥AB于P1点.
∴CO=OP1以O为圆心,OC为半径作⊙O,⊙O与AB相切,切点为P1,与CB的交点为D.
设CO=t,则OP1=t,CD=2t,OB=4-t.
由△ABC∽△OBP1,得
 ,
,
∴ =
= ,
,
解得:t=1.5,
∴CD=3,
∴当Q与点D重合时,以CQ为直径的圆与AB相切,切点为P1,连CP1、P1Q,△CP1Q为直角三角形,此时共有两个直角三角形,
当Q点在线段CD上时(不与C、D重合),0<CQ<3,CQ为直径的圆与AB相离,此时只有一个直角三角形CQP.
当Q点在DB上时(不与D、B重合),3<CQ<4,以CQ为直径的圆与AB有两个交点P2、P3.分别连接P2、P3与点C和Q,得直角三角形CQP2和CQP3,此时有三个直角三角形.
分析:(1)当CP为等腰三角形的底边时作CP的垂直平分线,交BC于Q,则△CPQ为等腰三角形;当CP为腰时,在BC上截取CQ=CP即可,所以这样的点有两个,分别求出即可;
(2)根据题意画出符合条件的三角形即可求出Q的位置,进而求出出相应的CQ的长;
(3)过Q作QP⊥BC,交AB于P点,连接CP,则△CPQ为直角三角形,作∠CAB的平分线AO,交BC于O点.作OP1⊥AB于P1点.设CO=t,则OP1=t,CD=2t,OB=4-t.先根据相似三角形△ABC∽△OBP1的性质求得t值,即得到线段CD的长度,再分情况讨论.①Q与点D重合时,以CQ为直径的圆与AB相切,②Q点在线段CD上时(不与C、D重合),0<CQ<3,以CQ为直径的圆与AB相离,③Q点在DB上时(不与D、B重合),3<CQ<4,以CQ为直径的圆与AB有两个交点P2、P3.
点评:本题考查了直角三角形的性质,等腰三角形的判定和性质以及相似三角形的性质和判定,此类题目还是相似与圆的知识的综合运用,难点在第(3)题,解决的根据是三角形相似的性质和直线和圆的三种位置关系.
则腰是CQ=PQ;
此时CQ=
 BC=1.5;
BC=1.5;当CP为腰时,在BC上截取CQ=CP,
则腰是CP=CQ′,
此时CQ=CP=
 =2.4;
=2.4;(2)当P是AB的中点时,如图2,若△CPQ与△ABC相似,这时满足条件的点Q有3个,
①当△COQ∽△BCA,时,
∴
 =
= ,
,∴CQ=
 BC=2;
BC=2;
②△PQ′B∽△CAB时,
∴
 ,
,∵AP=BP=
 AB=2.5,BC=4,
AB=2.5,BC=4,∴
 ,
,∴BQ′=
 ,
,∴CQ′=4-
 =
= ;
;③△CPQ″∽△BCA时,
∴
 ,
,∴
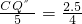 ,
,∴CQ″=
 ;
;(3)可能.
过Q作QP⊥BC,交AB于P点,连接CP,则△CPQ为直角三角形,作∠CAB的平分线AO,交BC于O点.作OP1⊥AB于P1点.
∴CO=OP1以O为圆心,OC为半径作⊙O,⊙O与AB相切,切点为P1,与CB的交点为D.
设CO=t,则OP1=t,CD=2t,OB=4-t.

由△ABC∽△OBP1,得
 ,
,∴
 =
= ,
,解得:t=1.5,
∴CD=3,
∴当Q与点D重合时,以CQ为直径的圆与AB相切,切点为P1,连CP1、P1Q,△CP1Q为直角三角形,此时共有两个直角三角形,
当Q点在线段CD上时(不与C、D重合),0<CQ<3,CQ为直径的圆与AB相离,此时只有一个直角三角形CQP.
当Q点在DB上时(不与D、B重合),3<CQ<4,以CQ为直径的圆与AB有两个交点P2、P3.分别连接P2、P3与点C和Q,得直角三角形CQP2和CQP3,此时有三个直角三角形.
分析:(1)当CP为等腰三角形的底边时作CP的垂直平分线,交BC于Q,则△CPQ为等腰三角形;当CP为腰时,在BC上截取CQ=CP即可,所以这样的点有两个,分别求出即可;
(2)根据题意画出符合条件的三角形即可求出Q的位置,进而求出出相应的CQ的长;
(3)过Q作QP⊥BC,交AB于P点,连接CP,则△CPQ为直角三角形,作∠CAB的平分线AO,交BC于O点.作OP1⊥AB于P1点.设CO=t,则OP1=t,CD=2t,OB=4-t.先根据相似三角形△ABC∽△OBP1的性质求得t值,即得到线段CD的长度,再分情况讨论.①Q与点D重合时,以CQ为直径的圆与AB相切,②Q点在线段CD上时(不与C、D重合),0<CQ<3,以CQ为直径的圆与AB相离,③Q点在DB上时(不与D、B重合),3<CQ<4,以CQ为直径的圆与AB有两个交点P2、P3.
点评:本题考查了直角三角形的性质,等腰三角形的判定和性质以及相似三角形的性质和判定,此类题目还是相似与圆的知识的综合运用,难点在第(3)题,解决的根据是三角形相似的性质和直线和圆的三种位置关系.

练习册系列答案
相关题目
 如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AB边所在的直线为轴,将△ABC旋转一周,则所得几何体的表面积是( )
如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AB边所在的直线为轴,将△ABC旋转一周,则所得几何体的表面积是( )A、
| ||
| B、24π | ||
C、
| ||
| D、12π |
 22、如图所示,已知Rt△ABC中,AB=AC,BD平分∠ABC,CE⊥BD交BD延长线于E,BA、CE延长线相交于F点.
22、如图所示,已知Rt△ABC中,AB=AC,BD平分∠ABC,CE⊥BD交BD延长线于E,BA、CE延长线相交于F点. 10、如图,已知Rt△ABC中,∠C=90°∠A=36°,以C为圆心,CB为半径的圆交AB于P,则弧BP的度数是
10、如图,已知Rt△ABC中,∠C=90°∠A=36°,以C为圆心,CB为半径的圆交AB于P,则弧BP的度数是 已知Rt△ABC中,∠ACB=90°,CA=CB,点D在BC的延长线上,点E在AC上,且CD=CE,延长BE交AD于点F,求证:BF⊥AD.
已知Rt△ABC中,∠ACB=90°,CA=CB,点D在BC的延长线上,点E在AC上,且CD=CE,延长BE交AD于点F,求证:BF⊥AD.