题目内容
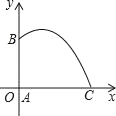
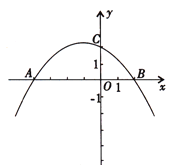
【题目】如图，抛物线
（
≠0）与
轴交于A(-4，0)，B（2，0），与
轴交与点C（0，2）．
(1)求抛物线的解析式；
(2)若点D为该抛物线上的一个动点，且在直线AC上方，当以A，C，D为顶点的三角形面积最大时，求点D的坐标及此时三角形的面积；
【答案】(1)y=﹣
x2﹣
x+2；(2)S△ADC的最大值为2，此时D（﹣2，2）．
【解析】
（1）根据A与B坐标设出抛物线解析式，将C坐标代入即可求出；
（2）过点D作DH⊥AB于点H，交直线AC于点G，连接DC，AD，如图所示，利用待定系数法求出直线AC解析式，设D横坐标为m，则有G横坐标也为m，表示出DH与GH，由DH-GH表示出DG，三角形ADC面积=三角形ADG面积+三角形DGC面积，表示出面积与m的关系式，利用二次函数性质确定出面积的最大值，以及此时m的值，即此时D的坐标即可．
(1)根据题意设抛物线解析式为y=a（x+4）（x﹣2），
把C（0，2）代入得：﹣8a=2，即a=﹣，
则抛物线解析式为y=﹣（x+4）（x﹣2）=﹣x2﹣x+2；
(2)过点D作DH⊥AB于点H，交直线AC于点G，连接DC，AD，如图所示，
设直线AC解析式为y=kx+t，则有
，
解得：
，
∴直线AC解析式为y=x+2，
设点D的横坐标为m，则G横坐标也为m，
∴DH=﹣m2﹣m+2，GH=m+2，
∴DG=﹣m2﹣m+2﹣m﹣2=﹣m2﹣m，
∴S△ADC=S△ADG+S△CDG=DGAH+DGOH=
DGAO=2DG=﹣m2﹣2m=﹣（m2+4m）=﹣ [（m+2）2﹣4]=﹣（m+2）2+2，
当m=﹣2时，S△ADC取得最大值2，此时yD=﹣×（﹣2）2﹣×（﹣2）+2=2，即D（﹣2，2）．
【题目】为了了解同学们对垃圾分类知识的知晓程度，增强同学们的环保意识，普及垃圾分类及投放的相关知识．某校环保社团的同学们设计了“垃圾分类知识及投放情况”的问卷，并在本校随机抽取了若干名同学进行了问卷测试，根据测试成绩分布情况，他们将全部成绩分成A，B，C，D四组，并绘制了如下不完整的统计图表：
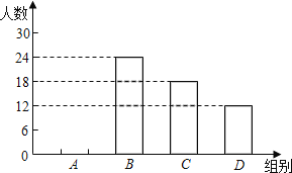
组别 | 分数段 | 频数 | 频率 |
A | 60≤x＜70 | a | b |
B | 70≤x＜80 | 24 | 0．4 |
C | 80≤x＜90 | 18 | c |
D | 90≤x＜100 | 12 | 0．2 |
请根据上述统计图表，解答下列问题：
（1）共抽取了多少名学生进行问卷测试？
（2）补全频数分布直方图；
（3）如果测试成绩不低于80分者为“优秀”，请你估计全校2000名学生中，“优秀”等次的学生约有多少人？
