题目内容
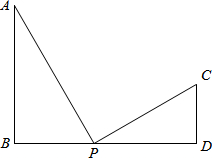（2013•永州）如图，已知AB⊥BD，CD⊥BD（1）若AB=9，CD=4，BD=10，请问在BD上是否存在P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似？若存在，求BP的长；若不存在，请说明理由；
（2）若AB=9，CD=4，BD=12，请问在BD上存在多少个P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似？并求BP的长；
（3）若AB=9，CD=4，BD=15，请问在BD上存在多少个P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似？并求BP的长；
（4）若AB=m，CD=n，BD=l，请问m，n，l满足什么关系时，存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的一个P点？两个P点？三个P点？
分析：（1）存在P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，设BP=x，根据∠B=∠D=90°和相似三角形的判定得出当
=
或
=
时，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，代入求出即可；
（2）存在P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，设BP=x，根据∠B=∠D=90°和相似三角形的判定得出当
=
或
=
时，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，代入求出即可；
（3）存在P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，设BP=x，根据∠B=∠D=90°和相似三角形的判定得出当
=
或
=
时，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，代入求出即可；
（4）存在P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，设BP=x，根据∠B=∠D=90°和相似三角形的判定得出当
=
或
=
时，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，代入后根据根的判别式进行判断即可．
| AB |
| CD |
| BP |
| PD |
| AB |
| PD |
| BP |
| CD |
（2）存在P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，设BP=x，根据∠B=∠D=90°和相似三角形的判定得出当
| AB |
| CD |
| BP |
| PD |
| AB |
| PD |
| BP |
| CD |
（3）存在P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，设BP=x，根据∠B=∠D=90°和相似三角形的判定得出当
| AB |
| CD |
| BP |
| PD |
| AB |
| PD |
| BP |
| CD |
（4）存在P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，设BP=x，根据∠B=∠D=90°和相似三角形的判定得出当
| AB |
| CD |
| BP |
| PD |
| AB |
| PD |
| BP |
| CD |
解答：解：（1）存在P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，
理由是：设BP=x，
∵AB⊥BD，CD⊥BD，
∴∠B=∠D=90°，
∴当
=
或
=
时，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，
∴①
=
或②
=
，
解方程①得：x=
，
方程②得：x（10-x）=36，
x2-10x+36=0，
△=（-10）2-4×1×36＜0，此方程无解，
∴当BP=
时，以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，
∴存在P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，此时BP的值为
；
（2）在BD上存在2个P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，
理由是：设BP=x，
∵AB⊥BD，CD⊥BD，
∴∠B=∠D=90°，
∴当
=
或
=
时，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，
∴①
=
或②
=
，
解方程①得：x=
，
方程②得：x（12-x）=36，
x2-12x+36=0，
△=（-12）2-4×1×36=0，
此方程的解为x2=x3=6，
∴当BP=
或6时，以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，
∴存在2个点P，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，此时BP的值为
或6；
（3）在BD上存在3个P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，
理由是：设BP=x，
∵AB⊥BD，CD⊥BD，
∴∠B=∠D=90°，
∴当
=
或
=
时，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，
∴①
=
或②
=
，
解方程①得：x=
，
方程②得：x（15-x）=36，
x2-15x+36=0，
△=（-15）2-4×1×36=81，
此方程的解为x2=3，x3=12，
∴当BP=
或3或12时，以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，
∴存在3个点P，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，此时BP的值为
或3或12；
（4）设BP=x，
∵AB⊥BD，CD⊥BD，
∴∠B=∠D=90°，
∴当
=
或
=
时，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，
∴①
=
或②
=
，
解方程①得：x=
，
方程②得：x（l-x）=mn，
x2-lx+mn=0，
△=（-l）2-4×1×mn=l2-4mn，
∴当l2-4mn＜0时，方程②没有实数根，
即当l2-4mn＜0时，存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的一个P点；
∵当l2-4mn=0时，方程②有1个实数根，
∴当l2-4mn=0时，存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的两个P点；
∵当l2-4mn＞0时，方程②有2个实数根，
∴当l2-4mn＞0时，存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的三个P点．
理由是：设BP=x，
∵AB⊥BD，CD⊥BD，
∴∠B=∠D=90°，
∴当
| AB |
| CD |
| BP |
| PD |
| AB |
| PD |
| BP |
| CD |
∴①
| 9 |
| 4 |
| x |
| 10-x |
| 9 |
| 10-x |
| x |
| 4 |
解方程①得：x=
| 90 |
| 13 |
方程②得：x（10-x）=36，
x2-10x+36=0，
△=（-10）2-4×1×36＜0，此方程无解，
∴当BP=
| 90 |
| 13 |
∴存在P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，此时BP的值为
| 90 |
| 13 |
（2）在BD上存在2个P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，
理由是：设BP=x，
∵AB⊥BD，CD⊥BD，
∴∠B=∠D=90°，
∴当
| AB |
| CD |
| BP |
| PD |
| AB |
| PD |
| BP |
| CD |
∴①
| 9 |
| 4 |
| x |
| 12-x |
| 9 |
| 12-x |
| x |
| 4 |
解方程①得：x=
| 108 |
| 13 |
方程②得：x（12-x）=36，
x2-12x+36=0，
△=（-12）2-4×1×36=0，
此方程的解为x2=x3=6，
∴当BP=
| 108 |
| 13 |
∴存在2个点P，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，此时BP的值为
| 108 |
| 13 |
（3）在BD上存在3个P点，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，
理由是：设BP=x，
∵AB⊥BD，CD⊥BD，
∴∠B=∠D=90°，
∴当
| AB |
| CD |
| BP |
| PD |
| AB |
| PD |
| BP |
| CD |
∴①
| 9 |
| 4 |
| x |
| 15-x |
| 9 |
| 15-x |
| x |
| 4 |
解方程①得：x=
| 135 |
| 13 |
方程②得：x（15-x）=36，
x2-15x+36=0，
△=（-15）2-4×1×36=81，
此方程的解为x2=3，x3=12，
∴当BP=
| 135 |
| 13 |
∴存在3个点P，使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似，此时BP的值为
| 135 |
| 13 |
（4）设BP=x，
∵AB⊥BD，CD⊥BD，
∴∠B=∠D=90°，
∴当
| AB |
| CD |
| BP |
| PD |
| AB |
| PD |
| BP |
| CD |
∴①
| m |
| n |
| x |
| l-x |
| m |
| l-x |
| x |
| n |
解方程①得：x=
| ml |
| m+n |
方程②得：x（l-x）=mn，
x2-lx+mn=0，
△=（-l）2-4×1×mn=l2-4mn，
∴当l2-4mn＜0时，方程②没有实数根，
即当l2-4mn＜0时，存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的一个P点；
∵当l2-4mn=0时，方程②有1个实数根，
∴当l2-4mn=0时，存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的两个P点；
∵当l2-4mn＞0时，方程②有2个实数根，
∴当l2-4mn＞0时，存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的三个P点．
点评：本题考查了相似三角形的判定和性质，根的判别式的应用，注意：ax2+bx+c=0（a≠0，a、b、c为常数），当△=b2-4ac＜0时，方程无实数解，当△=b2-4ac=0时，方程有两个相等的实数解，当△=b2-4ac＞0时，方程有两个不等的实数解．
练习册系列答案
阅读快车系列答案
相关题目
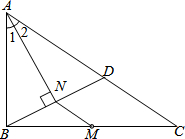（2013•永州）如图，M是△ABC的边BC的中点，AN平分∠BAC，BN⊥AN于点N，延长BN交AC于点D，已知AB=10，BC=15，MN=3
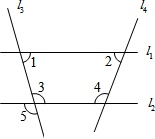（2013•永州）如图，下列条件中能判定直线l1∥l2的是（ ）
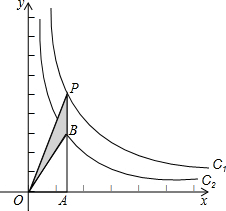（2013•永州）如图，两个反比例函数y=
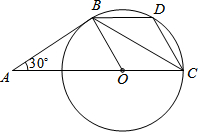（2013•永州）如图，AB是⊙O的切线，B为切点，圆心在AC上，∠A=30°，D为
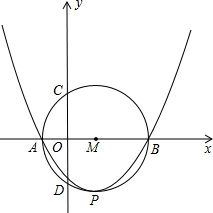（2013•永州）如图，已知二次函数y=（x-m）2-4m2（m＞0）的图象与x轴交于A、B两点．