题目内容
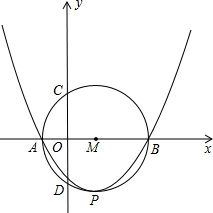 (2013•永州)如图,已知二次函数y=(x-m)2-4m2(m>0)的图象与x轴交于A、B两点.
(2013•永州)如图,已知二次函数y=(x-m)2-4m2(m>0)的图象与x轴交于A、B两点.(1)写出A、B两点的坐标(坐标用m表示);
(2)若二次函数图象的顶点P在以AB为直径的圆上,求二次函数的解析式;
(3)在(2)的基础上,设以AB为直径的⊙M与y轴交于C、D两点,求CD的长.
分析:(1)解关于x的一元二次方程(x-m)2-4m2=0,求出x的值,即可得到A、B两点的坐标;
(2)由二次函数图象的顶点P在以AB为直径的圆上,A、B是抛物线与x轴的交点,根据抛物线的对称性及圆的半径处处相等可知PM是AB的垂直平分线,且MP=MA=MB=
AB,得出点P的坐标为(m,-2m),又根据二次函数的顶点式为y=(x-m)2-4m2(m>0),得出顶点P的坐标为:(m,-4m2),则-2m=-4m2,解方程求出m的值,再把m的值代入y=(x-m)2-4m2,即可求出二次函数的解析式;
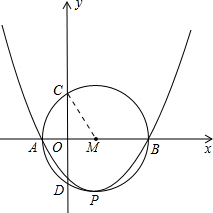
(3)连接CM.根据(2)中的结论,先在Rt△OCM中,求出CM,OM的长度,利用勾股定理列式求出OC的长,再根据垂径定理得出弦CD的长等于OC的2倍.
(2)由二次函数图象的顶点P在以AB为直径的圆上,A、B是抛物线与x轴的交点,根据抛物线的对称性及圆的半径处处相等可知PM是AB的垂直平分线,且MP=MA=MB=
| 1 |
| 2 |
(3)连接CM.根据(2)中的结论,先在Rt△OCM中,求出CM,OM的长度,利用勾股定理列式求出OC的长,再根据垂径定理得出弦CD的长等于OC的2倍.
解答:解:(1)∵y=(x-m)2-4m2,
∴当y=0时,(x-m)2-4m2=0,
解得x1=-m,x2=3m,
∵m>0,
∴A、B两点的坐标分别是(-m,0),(3m,0);
(2)∵A(-m,0),B(3m,0),m>0,
∴AB=3m-(-m)=4m,圆的半径为
AB=2m,
∴OM=AM-OA=2m-m=m,
∴抛物线的顶点P的坐标为:(m,-2m),
又∵二次函数y=(x-m)2-4m2(m>0)的顶点P的坐标为:(m,-4m2),
 ∴-2m=-4m2,
∴-2m=-4m2,
解得m1=
,m2=0(舍去),
∴二次函数的解析式为y=(x-
)2-1,即y=x2-x-
;
(3)如图,连接CM.
在Rt△OCM中,∵∠COM=90°,CM=2m=2×
=1,OM=m=
,
∴OC=
=
=
,
∴CD=2OC=
.
∴当y=0时,(x-m)2-4m2=0,
解得x1=-m,x2=3m,
∵m>0,
∴A、B两点的坐标分别是(-m,0),(3m,0);
(2)∵A(-m,0),B(3m,0),m>0,
∴AB=3m-(-m)=4m,圆的半径为
| 1 |
| 2 |
∴OM=AM-OA=2m-m=m,
∴抛物线的顶点P的坐标为:(m,-2m),
又∵二次函数y=(x-m)2-4m2(m>0)的顶点P的坐标为:(m,-4m2),
 ∴-2m=-4m2,
∴-2m=-4m2,解得m1=
| 1 |
| 2 |
∴二次函数的解析式为y=(x-
| 1 |
| 2 |
| 3 |
| 4 |
(3)如图,连接CM.
在Rt△OCM中,∵∠COM=90°,CM=2m=2×
| 1 |
| 2 |
| 1 |
| 2 |
∴OC=
| CM2-OM2 |
12-(
|
| ||
| 2 |
∴CD=2OC=
| 3 |
点评:本题是二次函数的综合题,其中涉及到二次函数与一元二次方程的关系,二次函数的性质,以及圆的半径、弦心距、半弦长构成直角三角形的应用,勾股定理,垂径定理等知识,综合性较强,但难度不是很大,仔细分析求解便不难解决.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
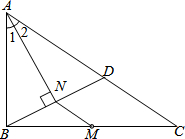 (2013•永州)如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
(2013•永州)如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3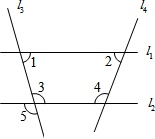 (2013•永州)如图,下列条件中能判定直线l1∥l2的是( )
(2013•永州)如图,下列条件中能判定直线l1∥l2的是( )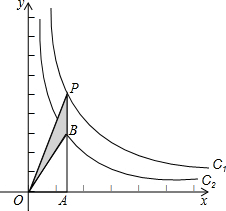 (2013•永州)如图,两个反比例函数y=
(2013•永州)如图,两个反比例函数y=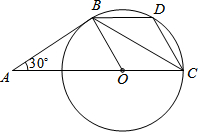 (2013•永州)如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=30°,D为
(2013•永州)如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=30°,D为