题目内容
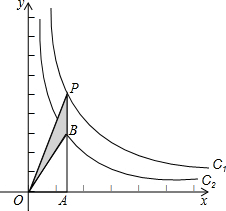 (2013•永州)如图,两个反比例函数y=
(2013•永州)如图,两个反比例函数y=| 4 |
| x |
| 2 |
| x |
1
1
.分析:根据反比例函数y=
(k≠0)系数k的几何意义得到S△POA=
×4=2,S△BOA=
×2=1,然后利用S△POB=S△POA-S△BOA进行计算即可.
| k |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵PA⊥x轴于点A,交C2于点B,
∴S△POA=
×4=2,S△BOA=
×2=1,
∴S△POB=2-1=1.
故答案为1.
∴S△POA=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△POB=2-1=1.
故答案为1.
点评:本题考查了反比例函数y=
(k≠0)系数k的几何意义:从反比例函数y=
(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
| k |
| x |
| k |
| x |

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
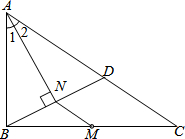 (2013•永州)如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
(2013•永州)如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3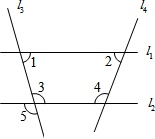 (2013•永州)如图,下列条件中能判定直线l1∥l2的是( )
(2013•永州)如图,下列条件中能判定直线l1∥l2的是( )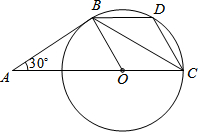 (2013•永州)如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=30°,D为
(2013•永州)如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=30°,D为
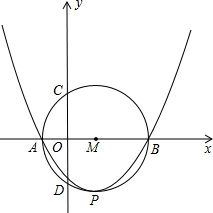 (2013•永州)如图,已知二次函数y=(x-m)2-4m2(m>0)的图象与x轴交于A、B两点.
(2013•永州)如图,已知二次函数y=(x-m)2-4m2(m>0)的图象与x轴交于A、B两点.