题目内容
8、已知点P是半径为5的⊙O内的一个定点，且OP=3，则过点P的所有弦中，弦长为整数的弦共有多少条（ ）
分析：先求出过P点的弦长的取值范围，然后判断出弦长为整数的弦有几条．
解答：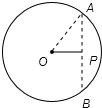
解：如图；过P作弦AB⊥OP，交⊙O于A、B；连接OA；
Rt△OAP中，OP=3，OA=5；
根据勾股定理，得AP=4；
∴AB=2AP=8；
故过点P的弦的长度都在8～10之间；
因此弦长为8、9、10；
当弦长为8、10时，过P点的弦分别为弦AB和过P点的直径，分别有一条；
当弦长为9时，根据圆的对称性知，符合条件的弦应该有两条；
故弦长为整数的弦共有4条．
故选C．
解：如图；过P作弦AB⊥OP，交⊙O于A、B；连接OA；Rt△OAP中，OP=3，OA=5；
根据勾股定理，得AP=4；
∴AB=2AP=8；
故过点P的弦的长度都在8～10之间；
因此弦长为8、9、10；
当弦长为8、10时，过P点的弦分别为弦AB和过P点的直径，分别有一条；
当弦长为9时，根据圆的对称性知，符合条件的弦应该有两条；
故弦长为整数的弦共有4条．
故选C．
点评：此题考查的是垂径定理及勾股定理的应用．需注意的是当弦长为9时，根据圆的对称性可得出两个符合条件的弦，不要漏解．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
已知点P是半径为5的圆O内一定点，且OP=4，则过点P的所有弦中，弦长可能取到的整数值为（ ）
| A、5，4，3 | B、10，9，8，7，6，5，4，3 | C、10，9，8，7，6 | D、12，11，10，9，8，7，6 |