题目内容
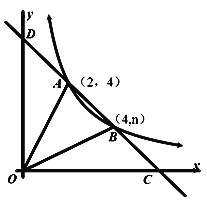
【题目】如图,直线y=ax+b与反比例函数![]() (x>0)的图象交于A(2,4),B(4,n)两点,与x轴,y轴分别交于C,D两点.
(x>0)的图象交于A(2,4),B(4,n)两点,与x轴,y轴分别交于C,D两点.
(1)求m,n的值;
(2)求ΔAOB的面积
(3)若线段CD上的点P到x轴,y轴的距离相等.求点P的坐标.
【答案】(1)m=8,n=2;
(2)ΔAOB的面积为6;
(3)点P的坐标(3,3).
【解析】分析:(1)由点A的坐标利用反比例函数图象上点的坐标特征即可得出m的值,再由点B也在反比例函数图象上即可得出n的值;(2)设过C、D点的直线解析式为y=kx+b,由点A、B的坐标利用待定系数法即可求出直线CD的解析式,求出点C点B的坐标,再利用![]() 求出ΔAOB的面积即可;(3)设出点P的坐标为(x,y),据(2)由点P到x轴、y轴的距离相等即可得出关于x的含绝对值符号的一元一次方程,解方程即可得出x的值,从而得出点P的坐标.
求出ΔAOB的面积即可;(3)设出点P的坐标为(x,y),据(2)由点P到x轴、y轴的距离相等即可得出关于x的含绝对值符号的一元一次方程,解方程即可得出x的值,从而得出点P的坐标.
本题解析: (1)将A(2,4)代入中得m=8,再代入B(4,n)中得n=2.
(2) 解:∵直线y=ax+b经过点A(2,4),B(4,2),
![]() 解得
解得![]()
C,D坐标为:C(6,0),D(0,6)
SΔAOB=SΔCOD-SΔAOD-SΔCOB=18-6-6=6
(3)当x=y时,x=-x+6,解得x=3,所以,P点坐标为(3,3).

练习册系列答案
相关题目