题目内容
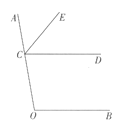
【题目】如图,点E为正方形ABCD的边BC所在直线上的一点,连接AE,过点C作CF⊥AE于F,连接BF.

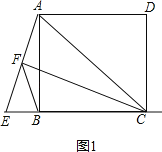
(1)如图1,当点E在CB的延长线上,且AC=EC时,求证:BF=![]() ;
;
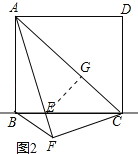
(2)如图2,当点E在线段BC上,且AE平分∠BAC时,求证:AB+BE=AC;
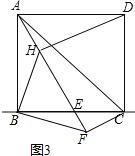
(3)如图3,当点E继续往右运动到BC中点时,过点D作DH⊥AE于H,连接BH.求证:∠BHF=45°.
【答案】见解析
【解析】
试题分析:(1)根据等腰三角形的性质和直角三角形斜边中线的性质即可证得结论;
(2)作EG⊥AC于G,根据角平分线的性质得出BE=EG,进而通过RT△ABE≌RT△AGE得出AG=AB,然后证得△EGC是等腰直角三角形,从而证得EG=GC,即可证得AB+BE=AC;
(3)设正方形的边长为1,则AB=AD=1,BE=EC=![]() ,根据勾股定理求得AE=
,根据勾股定理求得AE=![]() ,然后通过证得△AEB∽△CEF,△ADH∽△EAB,对应边成比例证得CF=AH=
,然后通过证得△AEB∽△CEF,△ADH∽△EAB,对应边成比例证得CF=AH=![]() ,然后根据SAS证得△ABH≌△CBF,证得BH=BF,∠ABH=∠CBF,从而证得△HBF是等腰直角三角形,从而证得∠BHF=45°.
,然后根据SAS证得△ABH≌△CBF,证得BH=BF,∠ABH=∠CBF,从而证得△HBF是等腰直角三角形,从而证得∠BHF=45°.
(1)证明:如图1,∵AC=EC,CF⊥AE,
∴AF=EF,
∴BF是RT△ABE的斜边的中线,
∴BF=![]() AE;
AE;
(2)如图2,作EG⊥AC于G,
∵AE平分∠BAC,AB⊥BE,
∴BE=EG,
在RT△ABE和RT△AGE中
![]() ,
,
∴RT△ABE≌RT△AGE(HL),
∴AG=AB,
∵四边形ABCD是正方形,
∴∠ACB=45°,
∴∠GEC=45°,
∴∠GEC=∠ACB=45°,
∴EG=GC,
∴AB+BE=AG+GC,
即AB+BE=AC;
(3)如图3,设正方形的边长为1,则AB=AD=1,
∵点E是BC中点,
∴BE=EC=![]() ,
,
∴AE=![]() =
=![]() ,
,
∵∠ABE=∠CFE=90°,∠AEB=∠CEF,
∴△AEB∽△CEF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CF=![]() ,
,
∵AD∥BC,
∴∠DAH=∠AEB,
∵∠AHD=∠BEA=90°,
∴△ADH∽△EAB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AH=![]() ,
,
∴CF=AH,
在△ABH和△CBF中
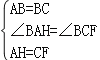
∴△ABH≌△CBF(SAS),
∴BH=BF,∠ABH=∠CBF,
∵∠ABH+∠HBE=∠ABE=90°,
∴∠HBF=90°,
∴△HBF是等腰直角三角形,
∴∠BHF=45°.