题目内容
【题目】如图，在平面直角坐标系中，已知 三角形ABC各顶点在格点上
（1）直接写出三角形ABC的三个顶点的坐标
A B C ；
（2）画出三角形ABC关于y轴对称的三角形A′B′C′.
（3）求三角形ABC的面积；
（4）直接与出A′C′与y轴交点的坐标 ．
【答案】（1）（2，2），（3，0），（5，4）；（2）作图见解析；（3）4；（4）（0，
）．
【解析】
（1）利用平面直角坐标系中点的坐标特征写出A、B、C三点的坐标；
（2）利用轴对称的性质找出A′、B′、C′点，然后连接即可；
（3）用一个矩形的面积分别减去三个直角三角形的面积可计算出△ABC的面积；
（4）先利用待定系数法求出直线A′C′的解析式，然后计算自变量为0所对应的自变量的值，从而得到直线A′C′与y轴交点的坐标．
解：（1）A、B、C点的坐标为（2，2），（3，0），（5，4）；
（2）如图，三角形A′B′C′为所作；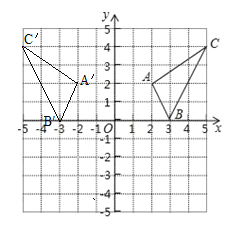
（3）三角形ABC的面积= 3×4-
×3×2-×4×2-×2×1=12-3-4-1=4；
（4）A′（-2，2），C′（-5，4），
设直线A′C′的解析式为y=kx+b，
把A′（-2，2），C′（-5，4）代入得
，
解得，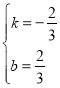
，即y=-x+，
∴直线A′C′与y轴的交点坐标为（0，）．
练习册系列答案
相关题目
