题目内容
 如图,AB与CD交于点O,OE⊥AB,OF⊥CD,若∠EOD=2∠BOD,求∠EOF的度数.
如图,AB与CD交于点O,OE⊥AB,OF⊥CD,若∠EOD=2∠BOD,求∠EOF的度数.解:∵OE⊥AB,
∴∠EOB=
90°
90°
,∴∠EOD+
∠BOD
∠BOD
=90°
90°
,又∵∠EOD=2∠BOD,
∴∠BOD=
30°
30°
,∠EOD=60°
60°
,∵OF⊥CD,
∴∠FOD=
90°
90°
,∴∠EOF=
90°
90°
-60°
60°
=30°
30°
.分析:根据OE⊥AB,可得∠EOD+∠BOD=90°,然后根据∠EOD=2∠BOD,求出∠BOD和∠EOD的度数,然后根据OF⊥CD,可求得∠EOF的度数.
解答:解:∵OE⊥AB,
∴∠EOB=90°,
∴∠EOD+∠BOD=90°,
又∵∠EOD=2∠BOD,
∴∠BOD=30°,∠EOD=60°,
∵OF⊥CD,
∴∠FOD=90°,
∴∠EOF=90°-60°=30°.
故答案为:90°,∠BOD,90°,30°,60°,90°,90°,60°,30°.
∴∠EOB=90°,
∴∠EOD+∠BOD=90°,
又∵∠EOD=2∠BOD,
∴∠BOD=30°,∠EOD=60°,
∵OF⊥CD,
∴∠FOD=90°,
∴∠EOF=90°-60°=30°.
故答案为:90°,∠BOD,90°,30°,60°,90°,90°,60°,30°.
点评:本题利用垂直的定义,对顶角和互补的性质计算,要注意领会由垂直得直角这一要点.

练习册系列答案
相关题目
 17、如图,AB与CD交于点P,CP=PD,∠A=40°,∠BPC=140°,∠D=70°,你能判断PC与PB的关系吗?请说明理由.
17、如图,AB与CD交于点P,CP=PD,∠A=40°,∠BPC=140°,∠D=70°,你能判断PC与PB的关系吗?请说明理由.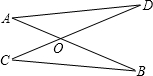 如图,AB与CD交于点O,OA=OC,OD=OB,根据
如图,AB与CD交于点O,OA=OC,OD=OB,根据 18、如图,AB与CD交于点O,OA=OC,OD=OB,∠AOD=
18、如图,AB与CD交于点O,OA=OC,OD=OB,∠AOD= 如图,AB与CD交于点O,OM为射线.
如图,AB与CD交于点O,OM为射线.