题目内容
附加题:如图,C是线段AB上一点,△ACD和△BCE都是等腰直角三角形,∠ADC=∠CEB=90°
(1)连接DE、M、N分别是AC、BC上一点,且∠MDC=∠CDE,∠NEC=∠CED,探索DM、DE、EN之间的数量关系,并说明理由.
(2)延长AD、BE交于F点,连接DE,CG⊥DE于G点,连接CF,CF与DE相交于O点,OC=OE,延长GC到H点,使得CH=CF,探索BF、BH的关系,并说明理由.

(1)连接DE、M、N分别是AC、BC上一点,且∠MDC=∠CDE,∠NEC=∠CED,探索DM、DE、EN之间的数量关系,并说明理由.
(2)延长AD、BE交于F点,连接DE,CG⊥DE于G点,连接CF,CF与DE相交于O点,OC=OE,延长GC到H点,使得CH=CF,探索BF、BH的关系,并说明理由.
分析:(1)根据等腰三角形性质求出∠DCE=90°,推行DM∥EN,过取DE的中点Q,连接CQ,根据梯形的中位线性质求出CQ=
DE=
(DM+EN),即可推出答案;
(2)根据互余两角的关系求出∠GCD=∠GEC=∠OCE,推出∠GCA=∠OCE=∠BCH,证△FBC≌△HBC即可.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据互余两角的关系求出∠GCD=∠GEC=∠OCE,推出∠GCA=∠OCE=∠BCH,证△FBC≌△HBC即可.
解答: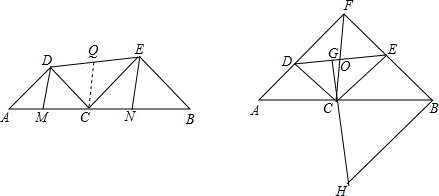 解:(1)DM+EN=DE,
解:(1)DM+EN=DE,
理由是:∵等腰直角△ADC和△BEC,
∴∠DCA=45°,∠BCE=45°,
∴∠DCE=180°-45°-45°=90°,
∴∠CDE+∠CED=180°-90°,
∵∠MDC=∠CDE,∠NEC=∠CED,
∴∠MDC+∠CDE+∠DEC+∠NEC=2×90°=180°,
∴DM∥EN,
过取DE的中点Q,连接CQ,
∵∠DCE=90°,
∴CQ=QE=DQ,
∴∠QCE=∠QEC=∠NEC,
∴CQ∥EN,
同理CQ∥DM,
即DM∥CQ∥EN,
∵Q是DE的中点,
∴MC=CN,
∴CQ=
(DM+EN),
∵CQ=QD=QE=
DE,
∴DM+EN=DE.
(2)BF=BH,BF⊥BH,
理由是:由(1)证得:∠DCE=90°,
∵∠DCE=90°,CG⊥DE,
∴∠DCG+∠ECG=90°,∠ECG+∠GEC=90°,
∴∠DCG=∠GEC,
∵CO=OE,
∴∠GEC=∠ECO,
∴∠GCD=∠ECO,
∵的三角形△ACD和△BEC,
∴∠DCA=∠ECB=45°,
∴∠GCD+∠DCA=∠OCE+∠ECB,
即∠GCA=∠FCB,
∵∠GCA=∠BCH,
∴∠BCH=∠FCB,
在△FBC和△HBC中
,
∴△FBC≌△HBC,
∴BF=BH,∠FBC=∠HBC=45°,
∴∠FBH=45°+45°=90°,
∴FB⊥BH.
 解:(1)DM+EN=DE,
解:(1)DM+EN=DE,理由是:∵等腰直角△ADC和△BEC,
∴∠DCA=45°,∠BCE=45°,
∴∠DCE=180°-45°-45°=90°,
∴∠CDE+∠CED=180°-90°,
∵∠MDC=∠CDE,∠NEC=∠CED,
∴∠MDC+∠CDE+∠DEC+∠NEC=2×90°=180°,
∴DM∥EN,
过取DE的中点Q,连接CQ,
∵∠DCE=90°,
∴CQ=QE=DQ,
∴∠QCE=∠QEC=∠NEC,
∴CQ∥EN,
同理CQ∥DM,
即DM∥CQ∥EN,
∵Q是DE的中点,
∴MC=CN,
∴CQ=
| 1 |
| 2 |
∵CQ=QD=QE=
| 1 |
| 2 |
∴DM+EN=DE.
(2)BF=BH,BF⊥BH,
理由是:由(1)证得:∠DCE=90°,
∵∠DCE=90°,CG⊥DE,
∴∠DCG+∠ECG=90°,∠ECG+∠GEC=90°,
∴∠DCG=∠GEC,
∵CO=OE,
∴∠GEC=∠ECO,
∴∠GCD=∠ECO,
∵的三角形△ACD和△BEC,
∴∠DCA=∠ECB=45°,
∴∠GCD+∠DCA=∠OCE+∠ECB,
即∠GCA=∠FCB,
∵∠GCA=∠BCH,
∴∠BCH=∠FCB,
在△FBC和△HBC中
|
∴△FBC≌△HBC,
∴BF=BH,∠FBC=∠HBC=45°,
∴∠FBH=45°+45°=90°,
∴FB⊥BH.
点评:本题考查了梯形的中位线,等腰三角形的性质,等腰直角三角形性质,全等三角形的性质和判定,平行线的性质和判定等知识点的应用,解(1)的关键是求出CQ是梯形的中位线,解(2)小题的关键是证出∠FCB=∠HCB,本题综合性比较强,主要检查学生能否综合运用性质进行推理,题型较好,通过做此题培养了学生分析问题和解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
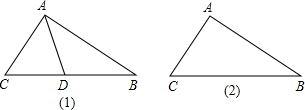 附加题,如图,在△ABC中,∠C=2∠B.
附加题,如图,在△ABC中,∠C=2∠B. 27、附加题:
27、附加题: 附加题,如图,在△ABC中,∠C=2∠B.
附加题,如图,在△ABC中,∠C=2∠B.