题目内容
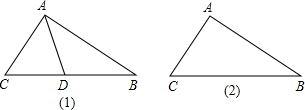 附加题,如图,在△ABC中,∠C=2∠B.
附加题,如图,在△ABC中,∠C=2∠B.(1)AD是△ABC的角平分线,求证:AB=AC+CD.
(2)若AD是△ABC的外角平分线交BC的延长线于D,其它条件不变,线段AB,AC,CD之间有什么确定的数量关系?画图并证明你的结论.
分析:(1)在AB上取一点E,使得AE=AC,连接DE,证明△ACD≌△AED,得出CD=DE,及证明△EDB为等腰三角形,得出DE=BE,得出AB=AC+CD;
(2)在AB的延长线AF上取一点E,使得AE=AC,连接DE.证明△ACD≌△AED,DE=BE,BE=CD,得出结论.
(2)在AB的延长线AF上取一点E,使得AE=AC,连接DE.证明△ACD≌△AED,DE=BE,BE=CD,得出结论.
解答: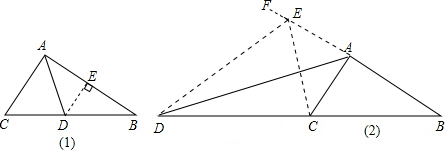 (1)证明:在AB上取一点E,使得AE=AC,连接DE
(1)证明:在AB上取一点E,使得AE=AC,连接DE
在△ACD和△AED中
.
∴△ACD≌△AED
∴∠C=∠AED,CD=DE
又∵∠C=2∠B
∴∠AED=2∠B
又∵∠AED=∠B+∠EDB
∴DE=BE
∴BE=CD
∴AB=AC+CD
(2)AB=CD-AC
证明:在BA的延长线AF上取一点E,使得AE=AC,连接DE
在△ACD和△AED中
∵
.
∴△ACD≌△AED
∴∠ACD=∠AED,CD=DE
∴∠ACB=∠FED
又∵∠ACB=2∠B
∴∠FAD=2∠B
又∵∠FED=∠B+∠EDB
∴∠EDB=∠B
∴DE=BE
∴BE=CD
∴AB=CD-AC.
 (1)证明:在AB上取一点E,使得AE=AC,连接DE
(1)证明:在AB上取一点E,使得AE=AC,连接DE在△ACD和△AED中
|
∴△ACD≌△AED
∴∠C=∠AED,CD=DE
又∵∠C=2∠B
∴∠AED=2∠B
又∵∠AED=∠B+∠EDB
∴DE=BE
∴BE=CD
∴AB=AC+CD
(2)AB=CD-AC
证明:在BA的延长线AF上取一点E,使得AE=AC,连接DE
在△ACD和△AED中
∵
|
∴△ACD≌△AED
∴∠ACD=∠AED,CD=DE
∴∠ACB=∠FED
又∵∠ACB=2∠B
∴∠FAD=2∠B
又∵∠FED=∠B+∠EDB
∴∠EDB=∠B
∴DE=BE
∴BE=CD
∴AB=CD-AC.
点评:本题考查了全等三角形的判定、三角形的角平分线的性质及三角形内外角的关系;正确作出辅助线是解答本题的关键,证明线段的和差问题往往是通过全等来证明的.

练习册系列答案
相关题目
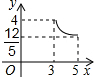
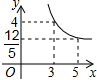
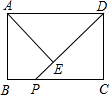 附加题:如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连接DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是( )
附加题:如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连接DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是( )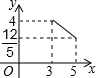
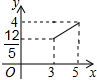
 27、附加题:
27、附加题: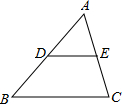 附加题:如图,在△ABC中,BC=2,则中位线DE=
附加题:如图,在△ABC中,BC=2,则中位线DE= 附加题:
附加题: (附加题)如图,在一块三角形区域土地ABC中,∠C=90°,AC=8,BC=6,底边AB上的高h=
(附加题)如图,在一块三角形区域土地ABC中,∠C=90°,AC=8,BC=6,底边AB上的高h=