题目内容
【题目】如图,四边形![]() 为正方形.在边
为正方形.在边![]() 上取一点
上取一点![]() ,连接
,连接![]() ,使
,使![]() .
.
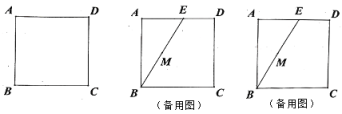
(1)利用尺规作图(保留作图痕迹):分别以点![]() 、
、![]() 为圆心,
为圆心,![]() 长为半径作弧交正方形内部于点
长为半径作弧交正方形内部于点![]() ,连接
,连接![]() 并延长交边
并延长交边![]() 于点
于点![]() ,则
,则![]() ;
;
(2)在前面的条件下,取![]() 中点
中点![]() ,过点
,过点![]() 的直线分别交边
的直线分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
①当![]() 时,求证:
时,求证:![]() ;
;
②当![]() 时,延长
时,延长![]() ,
,![]() 交于
交于![]() 点,猜想
点,猜想![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)作图见解析;(2)①见解析;②数量关系为:![]() 或
或![]() .理由见解析;
.理由见解析;
【解析】
(1)按照题意,尺规作图即可;
(2)连接PE,先证明PQ垂直平分BE,得到PB=PE,再证明![]() ,得到
,得到![]() ,利用在直角三角形中,30°所对的直角边等于斜边的一半,即可解答;
,利用在直角三角形中,30°所对的直角边等于斜边的一半,即可解答;
(3)NQ=2MQ或NQ=MQ,分两种情况讨论,作辅助线,证明![]() ,即可解答.
,即可解答.
(1)如图1,分别以点![]() 、
、![]() 为圆心,
为圆心,![]() 长为半径作弧交正方形内部于点
长为半径作弧交正方形内部于点![]() ,连接
,连接![]() 并延长交边
并延长交边![]() 于点
于点![]() ;
;
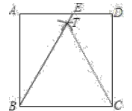
图1
(2)①连接![]() ,如图2,
,如图2,

图2
![]() 点
点![]() 是
是![]() 的中点,
的中点,![]()
![]()
![]() 垂直平分
垂直平分![]() .
.
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
②数量关系为:![]() 或
或![]() .
.
理由如下,分两种情况:
I、如图3所示,过点![]() 作
作![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,则
,则![]() .
.

图3
![]() 正方形
正方形![]() 中,
中,![]() ,
,
![]()
![]() .
.
在![]() 和
和![]() 中,
中,
![]()
![]()
![]()
![]() .
.
![]()
![]() .
.
又![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.![]()
![]() .
.
![]()
![]() .
.
Ⅱ、如图4所示,过点![]() 作
作![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,则
,则![]() .
.
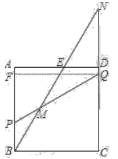
图4
同理可证![]() .
.
此时![]() .
.
又![]()
![]() ,
,![]() .
.
![]()
![]() .
.
![]()
![]() ,
,![]()
![]() .
.

 优等生题库系列答案
优等生题库系列答案【题目】)6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成如下统计图:
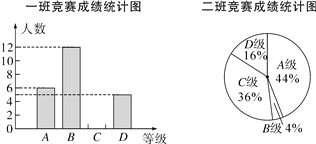
根据以上提供的信息解答下列问题:
(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a,b,c的值:
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | 87.6 | 80 | c |
(3)请从以下给出的三个方面对这次竞赛成绩的结果进行分析:
①从平均数和中位数方面比较一班和二班的成绩;
②从平均数和众数方面比较一班和二班的成绩;
③从B级以上(包括B级)的人数方面来比较一班和二班的成绩.