题目内容
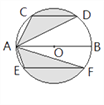
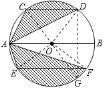
【题目】运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8.则图中阴影部分的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】作直径CG,连接OD、OE、OF、DG,则根据圆周角定理求得DG的长,证明DG=EF,则S扇形ODG=S扇形OEF,然后根据三角形的面积公式证明S△OCD=S△ACD,S△OEF=S△AEF,则S阴影=S扇形OCD+S扇形OEF=S扇形OCD+S扇形ODG=S半圆,即可求解.
作直径CG,连接OD、OE、OF、DG.
∵CG是圆的直径,
∴∠CDG=90°,则DG=![]() =8,
=8,
又∵EF=8,
∴DG=EF,
∴![]() ,
,
∴S扇形ODG=S扇形OEF,
∵AB∥CD∥EF,
∴S△OCD=S△ACD,S△OEF=S△AEF,
∴S阴影=S扇形OCD+S扇形OEF=S扇形OCD+S扇形ODG=S半圆=![]() π×52=
π×52=![]() ,
,
故选A.

练习册系列答案
相关题目
【题目】学校为了从李飞与刘亮中选取一人参加市射击比赛,现将他们某次射击训练的成绩绘制了如下图所示的折线统计图:
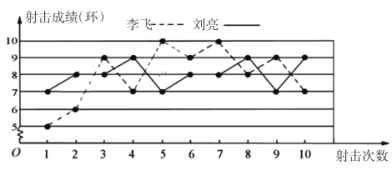
(1)请根据折线统计图中提供的信息填写下表:
平均数 | 中位 | 众数 | |
李飞 | 8 | ||
刘亮 | 8 | 8 |
(2)请计算李飞与刘亮射击训练的成绩的方差.(方差公式:![]() )
)
(3)从折线统计图上分析李飞与刘亮的射击成绩走势和稳定性,派谁去参加射击比赛更合适.