Question

【题目】在中，为直线上一点，为直线上一点，

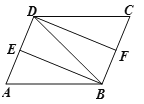
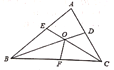
（1）如图1，当在上，在上时，求证；

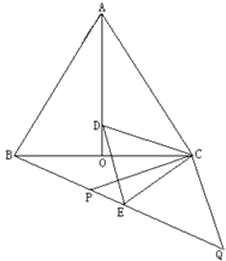
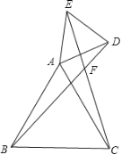
（2）如图2，当在的延长线上，在的延长线上时，点在上，连接，且，求证：

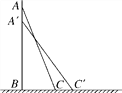
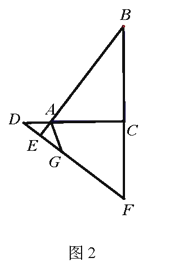
（3）如图3，在（2）的条件下，连接当平分时，将沿着折至探究与的数量关系．

Answer 1

【答案】（1）见解析（2）见解析（3）∠F＋2∠HGD＝90°，理由见解析

【解析】

（1）通过三角形内角和定理，可得∠AED＝∠ACB＝90°，可得结论；

（2）由直角三角形的性质和三角形内角和定理可得∠EAG＋∠AGE＝90°①，∠D＋∠F＝90°③，且2∠EAG∠D＝90°②，可以组成方程组，可得结论；

（3）由角平分线的性质和折叠的性质可得∠ADE＝2∠H，由外角性质可得∠ADE＝2∠DGH，由直角三角形的性质可得∠F＋2∠HGD＝90°．

（1）∵∠ADE＝∠B，∠A＝∠A，

且∠ADE＋∠A＋∠AED＝180°，∠B＋∠A＋∠ACB＝180°，

∴∠AED＝∠ACB＝90°，

∴DE⊥AB

（2）∵∠ADE＝∠B，∠DAE＝∠BAC，

∴∠AED＝∠ACB＝90°，

∴∠EAG＋∠AGE＝90°①，

∵∠EAG∠D＝45°，

∴2∠EAG∠D＝90°②，

∵∠D＋∠F＝90°③，

∴②＋③得：2∠EAG＋∠F＝180°④，

④①×2得：∠F2∠AGE＝0°，

∴∠F＝2∠AGE，

（3）如图3，

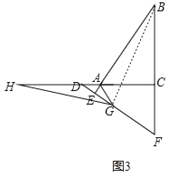
∵BG平分∠ABC，

∴∠ABG＝∠ABC，

∵将△AGB沿着AG折至△AGH，

∴∠H＝∠ABG＝∠ABC，

∵∠ADE＝∠B，

∴∠ADE＝2∠H，且∠ADE＝∠H＋∠DGH，

∴∠H＝∠DGH，

∴∠ADE＝2∠DGH，

∵∠F＋∠CDF＝90°，

∴∠F＋2∠HGD＝90°．