题目内容
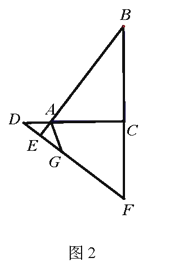
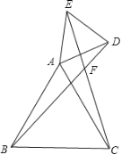
【题目】如图,已知△ABC和△ADE均为等边三角形,BD、CE交于点F.
(1)求证:BD=CE;(2)求锐角∠BFC的度数.
【答案】(1)证明见解析;(2)∠BFC=60°.
【解析】
(1)根据等边三角形的性质得出AE=AD,再由∠EAD+∠DAC=∠BAC+∠DAC,得出∠DAB=∠EAC,利用SAS可证得△EAC≌△DAB,从而可得出结论.
(2)根据△EAC≌△DAB可得∠ECA=∠DAB,从而在△BFC中可得∠ECA+∠FBC=60°,结合∠ACB=60°,利用三角形的内角和定理可得出∠BFC的度数.
(1)证明:∵△ABC和△ADE均为等边三角形,
∴AE=AD、AB=AC,
又∵∠EAD=∠BAC=60°,∠EAD+∠DAC=∠BAC+∠DAC,即∠DAB=∠EAC,
在△EAC和△DAB中,
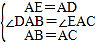 ,
,
∴△EAC≌△DAB,
即可得出BD=CE.
(2)由(1)△EAC≌△DAB,可得∠ECA=∠DBA,
又∵∠DBA+∠DBC=60°,
在△BFC中,∠ECA+∠DBC=60°,∠ACB=60°,
则∠BFC=180°-∠ACB-(∠ECA+∠DBC)=180°-60°-60°=60°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目