题目内容
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是线段
是线段![]() 上的一点,以
上的一点,以![]() 为腰在第二象限内作等腰直角
为腰在第二象限内作等腰直角![]() ,
,![]() .
.

(1)请直接写出点![]() ,
,![]() 的坐标:
的坐标:![]() ( , ),
( , ),![]() ( , );
( , );
(2)设点![]() 的坐标为
的坐标为![]() ,连接
,连接![]() 并延长交
并延长交![]() 轴于点
轴于点![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;
;![]() .
.
【解析】
(1)先令y=0求出x的值,再令x=0求出y的值即可得出A、B两点的坐标;
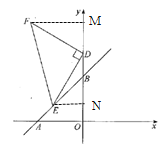
(2)过![]() 作
作![]() 轴于
轴于![]() ,根据AAS定理得出△DFM≌△EDN.故
,根据AAS定理得出△DFM≌△EDN.故![]()
![]() ,从而得出a、b的关系式,再根据点F在直线
,从而得出a、b的关系式,再根据点F在直线![]() 可得出结论;
可得出结论;
解:(1)当y=0时,x=-2,则A的坐标(-2,0),
当x=0时,y=2,则B的坐标(0,2),
![]() ,
,![]()
(2)过![]() 作
作![]() 轴于
轴于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,
,
∵∠FDM+∠EDN=90°,∠FDM+∠DFM=90°,
∴∠DFM=∠EDN,
在△DFM与△EDN中,
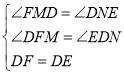
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() 在
在![]() 上,
上,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
使![]() 解析式为
解析式为![]() ,
,
![]() 代入得:
代入得:![]()
![]()
![]()
∴![]() ,
,
当y=0时,x=2;
∴![]() .
.

练习册系列答案
相关题目