题目内容
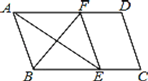
【题目】如图,在平行四边形ABCD中,作∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,连接EF.若AE=16,AF=10,则BF的长为( ).
A.10B.12C.14D.16
【答案】B
【解析】
先证明四边形ABEF是平行四边形,再证明邻边相等即可得出四边形ABEF是菱形,得出AE⊥BF,OA=OE,![]() ,由勾股定理求出OF,即可得出BF的长;
,由勾股定理求出OF,即可得出BF的长;
解:作标记如图所示:
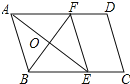
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵∠BAD的平分线交BC于点E,
∴∠DAE=∠BAE,
∴∠BAE=∠BEA,
∴AB=BE,同理可得AB=AF,
∴AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形(邻边相等的平行四边形是菱形),
∴AE⊥BF,OA=OE,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故选C.

练习册系列答案
相关题目