题目内容
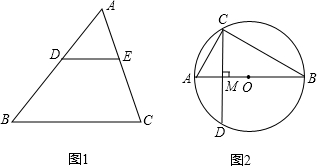 (1)如图1在△ABC中,D为AB上一点,DE∥BC交AC于点E,若AD:DB=2:3,BC=10,求DE的长.
(1)如图1在△ABC中,D为AB上一点,DE∥BC交AC于点E,若AD:DB=2:3,BC=10,求DE的长.(2)如图2,AB为⊙O的直径,弦CD⊥AB,垂足为点M,连接AC.若∠B=30°,AB=2,求CD的长.
分析:(1)求出AD:AB的值,根据平行线得出△ADE∽△ABC,得出
=
=
,代入求出即可.
(2)求出∠ACB=90°,求出AC和BC的长,根据三角形的面积公式求出CM,根据垂径定理求出CD=2CM,代入求出即可.
| DE |
| BC |
| AD |
| AB |
| 2 |
| 5 |
(2)求出∠ACB=90°,求出AC和BC的长,根据三角形的面积公式求出CM,根据垂径定理求出CD=2CM,代入求出即可.
解答:(1)解:∵
=
,
∴
=
,
∵DE∥BC,
∴△ADE∽△ABC,
∴
=
=
,
∵BC=10,
∴DE=4.
(2)解:∵AB为直径,
∴∠ACB=90°,
∵∠B=30°,
∴AC=
AB=1,
由勾股定理得:BC=
=
,
∵在Rt△ACB中,由面积公式得:
×AB×CM=
×AC×BC,
∴2×CM=1×
,
∴CM=
,
∵CD⊥AB,AB过圆心O,
∴由垂径定理得:CD=2CM=2×
=
,
答:CD的长是
.
| AD |
| DB |
| 2 |
| 3 |
∴
| AD |
| AB |
| 2 |
| 5 |
∵DE∥BC,
∴△ADE∽△ABC,
∴
| DE |
| BC |
| AD |
| AB |
| 2 |
| 5 |
∵BC=10,
∴DE=4.
(2)解:∵AB为直径,
∴∠ACB=90°,
∵∠B=30°,
∴AC=
| 1 |
| 2 |
由勾股定理得:BC=
| AB2-AC2 |
| 3 |
∵在Rt△ACB中,由面积公式得:
| 1 |
| 2 |
| 1 |
| 2 |
∴2×CM=1×
| 3 |
∴CM=
| ||
| 2 |
∵CD⊥AB,AB过圆心O,
∴由垂径定理得:CD=2CM=2×
| ||
| 2 |
| 3 |
答:CD的长是
| 3 |
点评:本题考查了平行线分线段成比例定理、勾股定理、垂径定理、三角形的面积等知识点,主要考查学生运用定理进行推理和计算的能力,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
相关题目
 16、如图,在①AB=AC ②AD=AE ③∠B=∠C ④BD=CE四个条件中,能证明△ABD与△ACE全等的条件顺序是( )
16、如图,在①AB=AC ②AD=AE ③∠B=∠C ④BD=CE四个条件中,能证明△ABD与△ACE全等的条件顺序是( ) 34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2, 16、如图,在AB、AC上各取一点D、E,使得AE=AD,连接CD、BE相交于点O,再连接AO.若∠CAO=∠BAO,则图中全等三角形共有( )
16、如图,在AB、AC上各取一点D、E,使得AE=AD,连接CD、BE相交于点O,再连接AO.若∠CAO=∠BAO,则图中全等三角形共有( ) 18、如图,在AB∥CD,∠A=40°,∠C=80°.求∠E的度数.
18、如图,在AB∥CD,∠A=40°,∠C=80°.求∠E的度数. 如图,在AB、AC上各取一点E、D,使AE=AD,连接BD、CE相交于点O,再连接AO、BC,若∠1=∠2,则图中全等三角形共有( )
如图,在AB、AC上各取一点E、D,使AE=AD,连接BD、CE相交于点O,再连接AO、BC,若∠1=∠2,则图中全等三角形共有( )