题目内容
一条弦把圆分成2:3两部分,那么这条弦所对的圆周角的度数为_______
72°或108°
先求出这条弦所对圆心角的度数,然后分情况讨论这条弦所对圆周角的度数.
解:如图,连接OA、OB.

弦AB将⊙O分为2:3两部分,
则∠AOB= ×360°=144°;
×360°=144°;
∴∠ACB= ∠AOB=72°,
∠AOB=72°,
∠ADB=180°-∠ACB=108°;
故这条弦所对的圆周角的度数为72°或108°.
解:如图,连接OA、OB.

弦AB将⊙O分为2:3两部分,
则∠AOB=
 ×360°=144°;
×360°=144°;∴∠ACB=
 ∠AOB=72°,
∠AOB=72°,∠ADB=180°-∠ACB=108°;
故这条弦所对的圆周角的度数为72°或108°.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目

 ,经过A、B的直线
,经过A、B的直线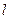 以每秒1个单位的速度向下作匀速平移运动,与此同时,点P从点B出发,在直线l上以每秒1个单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
以每秒1个单位的速度向下作匀速平移运动,与此同时,点P从点B出发,在直线l上以每秒1个单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.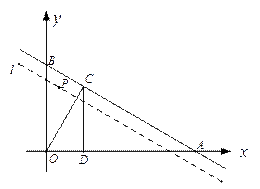
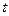 的代数式表示点P的坐标;
的代数式表示点P的坐标;
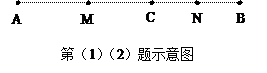

 ,半径为2cm的
,半径为2cm的 切
切 于点
于点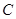 ,若将
,若将 上向右滚动,则当滚动到
上向右滚动,则当滚动到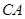 也相切时,圆心
也相切时,圆心 移动的水平距离是__________cm
移动的水平距离是__________cm