题目内容
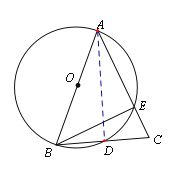
【题目】已知：如图，
为
的直径，
交
于点
，
交
于点
．
（1）求
的度数；
（2）求证：
．
【答案】（1）∠EBC=22．5°；（2）证明过程见解析．
【解析】
试题分析：(1)、由AB=AC，∠A=45°，可求出∠ABC的度数，由AB是直径可得∠AEB的度数，从而可得∠ABE的度数，继而可得∠EBC的度数；(2)、连接AD，由AB是直径，可得∠ADB=90°，在由AB=AC，由“三线合一”即可得证；
试题解析：(1)、∵∠BAC=45°，AB=AC，∴∠ABC=∠C=（180°-∠A）÷2=67．5°，∵AB是直径，∴∠AEB=90°，∴∠ABE=45°，∴∠EBC=∠ABC-∠ABE=22．5°；
(2)、连接AD，∵AB是直径，∴∠ADB=90°，由∵AB=AC，∴BD=CD．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
【题目】小慧根据学习函数的经验，对函数
的图象与性质进行了研究，下面是小慧的研究过程，请补充完成：
（1）函数
的自变量
的取值范围是__________；
（2）列表，找出
与
的几组对应值.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中， 
__________；
（3）在平面直角坐标系
中，描出以上表中各队对应值为坐标的点，并画出该函数的图象；
（4）写出该函数的一条性质：____________________________________________.
【题目】永州市是一个降水丰富的地区，今年4月初，某地连续降雨导致该地某水库水位持续上涨，下表是该水库4月1日~4月4日的水位变化情况：
日期x | 1 | 2 | 3 | 4 |
水位y(米) | 20．00 | 20．50 | 21．00 | 21．50 |
(1)请建立该水库水位y与日期x之间的函数模型；
(2)请用求出的函数表达式预测该水库今年4月6日的水位；
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗？
