题目内容
【题目】以直线![]() 上一点
上一点![]() 为端点作射线
为端点作射线![]() ,使
,使![]() ,将一块直角三角板的直角顶点放在
,将一块直角三角板的直角顶点放在![]() 处,一边
处,一边![]() 放在射线
放在射线![]() 上,将直角三角板
上,将直角三角板![]() 绕点
绕点![]() 逆时针方向旋转直至
逆时针方向旋转直至![]() 边第一次重合在射线
边第一次重合在射线![]() 上停止.
上停止.
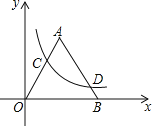
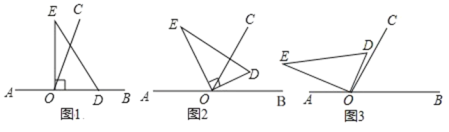
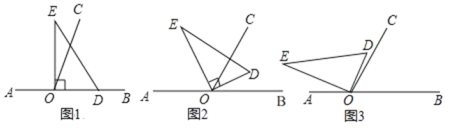
(1)如图1,边![]() 在射线
在射线![]() 上,则
上,则![]() ;
;
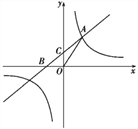
(2)如图2,若![]() 恰好平分
恰好平分![]() ,则
,则![]() ;
;
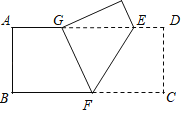
(3)如图3,若![]() ,则
,则![]() ;
;
(4)在旋转过程中,![]() 与
与![]() 始终保持的数量关系是 ,并请说明理由.
始终保持的数量关系是 ,并请说明理由.
【答案】(1)30![]() ;(2)30
;(2)30![]() ;(3)75
;(3)75![]() ;(4)∠COE∠BOD=30
;(4)∠COE∠BOD=30![]() ,理由见解析
,理由见解析
【解析】
(1)根据图形得出∠COE=∠DOE∠BOC,代入求出即可;
(2)根据角平分线定义求出∠AOC=2∠EOC=120![]() ,代入∠BOD=∠BOE∠DOE即可求解;
,代入∠BOD=∠BOE∠DOE即可求解;
(3)根据![]() ,先求出∠COD,再利用
,先求出∠COD,再利用![]() ∠COD+
∠COD+![]() 即可求解;
即可求解;
(4)根据各图的特点分别求解即可得到结论.
(1)∠COE=∠DOE∠BOC=90![]() 60
60![]() =30
=30![]() ,
,
故答案为:30![]() ;
;
(2)∵![]() 恰好平分
恰好平分![]() ,∠BOC=60
,∠BOC=60![]() ,
,
∴∠AOC=2∠EOC=120![]() ,∴∠EOC=60
,∴∠EOC=60![]() ,
,
∴∠BOE=∠EOC+∠BOC=120![]()
∵∠DOE=90![]() ,
,
∴∠BOD=∠BOE∠DOE=30![]()
故答案为:30![]() ;
;
(3)∵![]()
∴∠COD=![]()
∴![]() ∠COD+
∠COD+![]() =75
=75![]()
故答案为:75![]() ;
;
(4)∠COE∠BOD=30![]() ,理由如下:
,理由如下:
如图1,∠COE∠BOD=30![]() -0
-0![]() =30
=30![]() ;
;
如图2,∵∠BOD+∠COD=∠BOC=60![]() ,∠COE+∠COD=∠DOE=90
,∠COE+∠COD=∠DOE=90![]() ,
,
∴(∠COE+∠COD)(∠BOD+∠COD)
=∠COE+∠COD∠BOD∠COD
=∠COE∠BOD
=90![]() 60
60![]()
=30![]() ;
;
如图3,∵∠BOD-∠COD=∠BOC=60![]() ,∠COE-∠COD=∠DOE=90
,∠COE-∠COD=∠DOE=90![]() ,
,
∴(∠COE-∠COD)(∠BOD-∠COD)
=∠COE-∠COD∠BOD+∠COD
=∠COE∠BOD
=90![]() 60
60![]()
=30![]() ;
;
即∠COE∠BOD=30![]() .
.

练习册系列答案
相关题目