题目内容
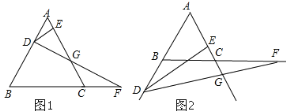
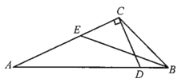
【题目】如图所示,已知在![]() 中,BE平分
中,BE平分![]() 交AC于点E,
交AC于点E,![]() 交AB于点D,
交AB于点D,![]() ,则
,则![]() 的度数为________.
的度数为________.
【答案】![]()
【解析】
由已知条件只能得到∠ACD=90°,由三角形外角性质可知∠BEA=∠ACD+∠BCD+∠CBE,因此求出∠BCD+∠CBE的度数即可得到答案;由垂直的定义及三角形内角和定理易得∠A+∠ABC+∠BCD=90°,结合角平分线的概念及∠BCD=∠A即可得到∠BCD+∠CBE的度数,进而可对题目进行解答.
∵CD⊥AC,
∴∠ACD=90°,
∴∠A+∠ABC+∠BCD=180°-∠ACD=90°.
∵BE平分∠ABC,
∴∠ABC=2∠CBE.
∵∠BCD=∠A,
∴∠A+∠ABC+∠BCD=2∠BCD+2∠CBE=90°,
∴∠BCD+∠CBE=45°,
∴∠BEA=∠ACD+∠BCD+∠CBE=135°.
故答案为:![]() .
.

练习册系列答案
相关题目