题目内容
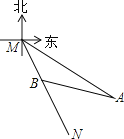
【题目】如图,射线MN表示一艘轮船的航行路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,A处到M处为100海里.
(1)求点A到航线MN的距离;
(2)在航线MN上有一点B,且∠MAB=15°,若轮船的速度为50海里/时,求轮船从M处到B处所用时间为多少小时?(结果保留根号)
【答案】(1)点A到航线MN的距离为50海里;(2)轮船从M处到B处所用时间约为(![]() ﹣1)小时.
﹣1)小时.
【解析】
(1)过A作AH⊥MN于H.由方向角的定义可知∠QMB=30°,∠QMA=60°,那么∠NMA=∠QMA﹣∠QMB=30°.解直角△AMH中,得出AH=![]() AM,问题得解;
AM,问题得解;
(2)先根据直角三角形两锐角互余求出∠HAM=60°,由∠MAB=15°,得出∠HAB=∠HAM﹣∠MAB=45°,那么△AHB是等腰直角三角形,求出BH=AH距离,然后根据时间=路程÷速度即可求解.
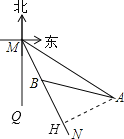
解:(1)如图,过A作AH⊥MN于H.
∵∠QMB=30°,∠QMA=60°,
∴∠NMA=∠QMA﹣∠QMB=30°.
在直角△AMH中,∵∠AHM=90°,∠AMH=30°,AM=100海里,
∴AH=![]() AM=50海里,
AM=50海里,
答:点A到航线MN的距离为50海里;
(2)在直角△AMH中,∵∠AHM=90°,∠AMH=30°,
∴∠HAM=60°,
∵∠MAB=15°,
∴∠HAB=∠HAM﹣∠MAB=45°,
∵∠AHB=90°,
∴BH=AH=50海里,
∵MH=![]() AH=50
AH=50![]() 海里,
海里,
∴MB=(50![]() ﹣50)海里,
﹣50)海里,
∴轮船从M处到B处所用时间为:![]() 小时,
小时,
答:轮船从M处到B处所用时间约为(![]() ﹣1)小时.
﹣1)小时.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目