题目内容
【题目】已知:如图,四边形ABCD为矩形,AB=10,BC=3,点E是CD的中点,点P在AB上以每秒2个单位的速度由A向B运动,(1)t为何值时,四边形PDEB是平行四边形?(2)点Q是直线AB上的动点,若以DEQP四点为顶点的四边形是菱形,求t值.
【答案】(1)t= ![]() ;(2)t= 2,4.5,0.5.
;(2)t= 2,4.5,0.5.
【解析】
(1)先求出CD,根据中点的性质求出DE=5,再由运动知BP=10-2t,进而由平行四边形的性质建立方程10-2t=5即可得出结论;
(2)分三种情况讨论,利用菱形的性质和勾股定理即可得出结论;
(1)∵四边形ABCD为矩形, AB=10,BC=3
∴CD=AB=10,AD=BC=3,
∵点E是CD的中点,
∴![]()
由运动知, AP=2t,
∴BP=ABAP=102t,
∵四边形PDEB是平行四边形,
∴PB=DE=5,
∴102t=5,
∴t=2.5;
(2)①当Q点在P的右边时,如图,
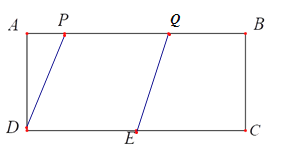
∵四边形DEQP为菱形,
∴DE=DP=PQ=5,
∴在Rt△ADP中,由勾股定理得:AP=4
∴2t=4;
∴t=2;
②当Q点在P的左边且在BC线段上时,如图,
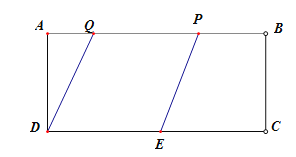
同①的方法得出![]()
![]() ,
,
2t=9;
t=4.5;
③当Q点在P的左边且在BC的延长线上时,如图,
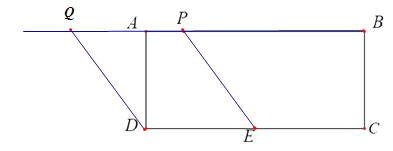
同①的方法得出,![]() ,
,![]()
2t=1,
![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目






