题目内容
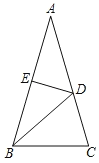
【题目】如图,已知![]() 是⊙O的直径,
是⊙O的直径,![]() ,点
,点![]() 在⊙O的半径
在⊙O的半径![]() 上运动,
上运动,![]() ,垂足为
,垂足为![]() ,
,![]() ,
,![]() 为⊙O的切线,切点为
为⊙O的切线,切点为![]() .
.
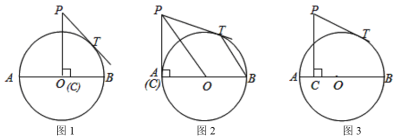
(1)如图1,当![]() 点运动到
点运动到![]() 点时,求
点时,求![]() 的长;
的长;
(2)如图2,当![]() 点运动到
点运动到![]() 点时,连接
点时,连接![]() 、
、![]() ,求证:
,求证:![]() ∥
∥![]() ;
;
(3)如图3,设![]() ,
,![]() ,求y与x的解析式并求出y的最小值.
,求y与x的解析式并求出y的最小值.
【答案】(1)6;(2)见解析;(3)![]() ,6
,6
【解析】
(1)连接OT,根据题意,由勾股定理可得出PT的长;
(2)连接OT,则OP平分劣弧AT,则∠AOP=∠B,从而证出结论;
(3)连接PO,由勾股定理可得PO=![]() ,再由勾股定理可得出PT =
,再由勾股定理可得出PT =![]() ,从而得出y与x之间的关系式y=
,从而得出y与x之间的关系式y=![]() ,进而求得y的最小值.
,进而求得y的最小值.
(1)连接OT
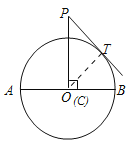
∵PC=10,OT=8,
∴由勾股定理得,PT=![]() =
=![]() =6;
=6;
(2)证明:连接OT ,
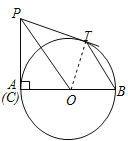
∵PT,PC为⊙O的切线,
∴OP平分劣弧AT,
∴∠POA=∠POT,
∵∠AOT=2∠B,
∴∠AOP=∠B,
∴PO∥BT
(3)连接PO,
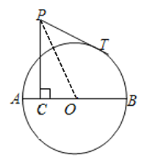
∵AB是⊙O的直径,![]() ,
,![]()
∴CO=8-x;
又∵![]()
∴![]() ,即
,即 ![]()
∴PO=![]()
∴y = PT =![]() =
=![]() =
=![]()
∴![]() ,
,
∴当x=8时,ymin=6

 智慧小复习系列答案
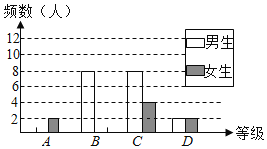
智慧小复习系列答案【题目】某校对九年级学生进行一次综合文科中考模拟测试,成绩x分(x为整数)评定为优秀、良好、合格、不合格四个等级(优秀、良好、合格、不合格分别用A、B、C、D表示),A等级:90≤x≤100,B等级:80≤x<90,C等级:60≤x<80,D等级:0≤x<60.该校随机抽取了一部分学生的成绩进行调查,并绘制成如图不完整的统计图表.
等级 | 频数(人数) | 频率 |
A | a | 20% |
B | 16 | 40% |
C | b | m |
D | 4 | 10% |
请你根据统计图表提供的信息解答下列问题:
(1)上表中的a ,b= ,m= .
(2)本次调查共抽取了多少名学生?请补全条形图.
(3)若从D等级的4名学生中抽取两名学生进行问卷调查,请用画树状图或列表的方法求抽取的两名学生恰好是一男一女的概率.