题目内容
【题目】如图,∠AOB=90°,在∠AOB的内部有一条射线OC.
(1)画射线OD⊥OC.
(2)写出此时∠AOD与∠BOC的数量关系,并说明理由.
【答案】
(1)解:如图所示:
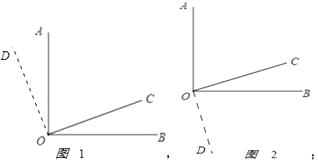
(2)解:如图1:
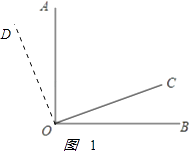 ,
,
∠AOD=∠BOC.
因为∠AOB=90°,
所以∠AOC+∠BOC=90°.
因为OD⊥OC,
所以∠AOD+∠AOC=90°.
所以∠AOD=∠BOC;
如图2:
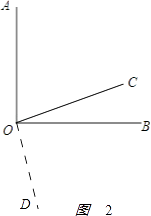 ,
,
∠AOD+∠BOC=180°.
因为∠AOD=∠AOC+∠BOC+∠BOD,
所以∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC
=∠AOB+∠COD=180°.
【解析】(1)根据垂线的定义,过直线上一点作已知线的垂线,此题两种情况,垂线作在OC的左边与右边;
(2)此题两种情况,![]() 当OD在OC左边时,根据同角的余角相等得出∠AOD=∠BOC,当OD在OC右边时,根据角的和差得出∠AOD+∠BOC=180°.
当OD在OC左边时,根据同角的余角相等得出∠AOD=∠BOC,当OD在OC右边时,根据角的和差得出∠AOD+∠BOC=180°.
【考点精析】本题主要考查了角的运算和垂线的性质的相关知识点,需要掌握角之间可以进行加减运算;一个角可以用其他角的和或差来表示;垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短才能正确解答此题.

练习册系列答案
相关题目
