Question

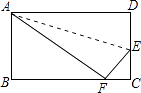
【题目】如图，在平面直角坐标系中，线段AB的两个端点为A、B分别在y轴正半轴、x轴负半轴上，直线CD分别交x轴正半轴、y轴负半轴于点C、D，且AB∥CD．

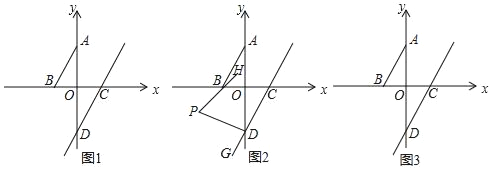
（1）如图1，若点A（0，a）和点B（b，0）的坐标满足

ⅰ）直接写出a、b的值，a＝_____，b＝_____；

ⅱ）把线段AB平移，使B点的对应点E到x轴距离为1，A点的对应点F到y轴的距离为2，且EF与两坐标轴没有交点，则F点的坐标为_____；

（2）若G是CD延长线上一点DP平分∠ADG，BH平分∠ABO，BH的反向延长线交DP于P（如图2），求∠HPD的度数；

（3）若∠BAO＝30°，点Q在x轴（不含点B、C）上运动，AM平分∠BAQ，QN平分∠AQC，（如图3）真接出∠BAM与∠NQC满足的数量关系．

Answer 1

【答案】（1）ⅰ），﹣1；ⅱ）（﹣2，+1）或（2，+1）；（2）45°；（3）当点Q在点B左侧时，∠BAM+∠NQC＝30°，当点Q在B、C之间时，∠NQC﹣∠BAM＝30°，当点Q在点C右侧时，∠BAM+∠NQC＝60°．

【解析】

（1）ⅰ）利用非负数的性质即可求解；

ⅱ）有两种情形，画出图象即可解决问题；

（2）设BH交y轴于K．∠ABK＝∠OBK＝α．利用三角形内角和定理，只要求出∠PKD，∠PDK即可解决问题；

（3）分三种情形画出图形分别求解即可解决问题；

解：（1）ⅰ）∵ ，

又|﹣a|≥0， ≥0，

∴a＝，b＝﹣1，

故答案为，﹣1．

ⅱ）如图1中，有两种情形，点F坐标为：（﹣2， +1）或（2， +1）．

故答案为（﹣2， +1）或（2， +1）．

（2）如图2中，设BH交y轴于K．∠ABK＝∠OBK＝α．

∵AB∥CD，

∴∠ABO＝∠OCD＝2α，

∴∠ODP＝ （90°+2α）＝45°+α．

∵∠BKO＝90°﹣α，

∴∠HPD＝180°﹣（90°﹣α）﹣（45°+α）＝45°．

（3）如图3﹣1中，当点Q在点B左侧时，∠BAM+∠NQC＝30°

如图3﹣2中，当点Q在B、C之间时，∠NQC﹣∠BAM＝30°．

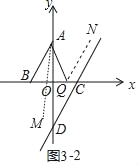
如图3﹣3中，当点Q在点C右侧时，∠BAM+∠NQC＝60°．

故答案为：（1）ⅰ），﹣1；ⅱ）（﹣2，+1）或（2，+1）；（2）45°；（3）当点Q在点B左侧时，∠BAM+∠NQC＝30°，当点Q在B、C之间时，∠NQC﹣∠BAM＝30°，当点Q在点C右侧时，∠BAM+∠NQC＝60°．