Question

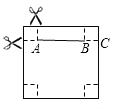
【题目】如图，将边长为40cm的正方形硬纸板的四个角各剪掉一个同样大小的正方形，剩余部分折成一个无盖的盒子．（纸板的厚度忽略不计）．

（1）若该无盖盒子的底面积为900cm2，求剪掉的正方形的边长；

（2）求折成的无盖盒子的侧面积的最大值．

Answer 1

【答案】（1）5cm；（2）最大值是800cm2．

【解析】

（1）设剪掉的正方形的边长为xcm，则AB=（40-2x）cm，根据盒子的底面积为484cm2，列方程解出即可；

（2）设剪掉的正方形的边长为xcm，盒子的侧面积为ycm2，侧面积=4个长方形面积；则y=-8x2+160x，配方求最值．

（1）设剪掉的正方形的边长为x cm，

则（40﹣2x）2＝900，

即40﹣2x＝±30，

解得x1＝35（不合题意，舍去），x2＝5；

答：剪掉的正方形边长为5cm；

（2）设剪掉的正方形的边长为x cm，盒子的侧面积为y cm2，

则y与x的函数关系式为y＝4（40﹣2x）x，

即y＝﹣8x2+160x，

y＝﹣8（x﹣10）2+800，

∵﹣8＜0，

∴y有最大值，

∴当x＝10时，y最大＝800；

答：折成的长方体盒子的侧面积有最大值，这个最大值是800cm2．