ЬтФПФкШн
ЁОЬтФПЁПдФЖСВФСЯЃКЯёЃЈ![]() +
+![]() ЃЉЃЈ
ЃЉЃЈ![]()
![]() ЃЉЃН3ЃЌ
ЃЉЃН3ЃЌ![]()
![]() ЃНaЃЈaЁн0ЃЉЃЌЃЈ
ЃНaЃЈaЁн0ЃЉЃЌЃЈ![]() +1ЃЉЃЈ
+1ЃЉЃЈ![]() Љ1ЃЉЃНbЉ1ЃЈbЁн0ЃЉЃЌЁЁЃЌетжжСНИіКЌЖўДЮИљЪНЕФДњЪ§ЪНЯрГЫЃЌЛ§ВЛКЌЖўДЮИљЪНЃЌЮвУЧГЦетСНИіДњЪ§ЪНЛЅЮЊгаРэЛЏвђЪНР§ШчЃК
Љ1ЃЉЃНbЉ1ЃЈbЁн0ЃЉЃЌЁЁЃЌетжжСНИіКЌЖўДЮИљЪНЕФДњЪ§ЪНЯрГЫЃЌЛ§ВЛКЌЖўДЮИљЪНЃЌЮвУЧГЦетСНИіДњЪ§ЪНЛЅЮЊгаРэЛЏвђЪНР§ШчЃК![]() гы
гы![]() ЃЌ
ЃЌ![]() +1гы
+1гы![]() Љ1ЃЌ2
Љ1ЃЌ2![]() +3
+3![]() гы2
гы2![]() Љ3
Љ3![]() ЕШЖМЪЧЛЅЮЊгаРэЛЏвђЪНЃЌдкНјааЖўДЮИљЪНМЦЫуЪБЃЌРћгУгаРэЛЏвђЪНЃЌПЩвдЛЏШЅЗжФИжаЕФИљКХЃЎ
ЕШЖМЪЧЛЅЮЊгаРэЛЏвђЪНЃЌдкНјааЖўДЮИљЪНМЦЫуЪБЃЌРћгУгаРэЛЏвђЪНЃЌПЩвдЛЏШЅЗжФИжаЕФИљКХЃЎ
Р§ШчЃК![]() ЃЛ
ЃЛ ЃЛ
ЃЛ
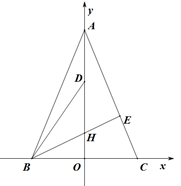
НтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉ3Љ![]() гыЁЁ ЁЁЛЅЮЊгаРэЛЏвђЪНЃЌНЋ
гыЁЁ ЁЁЛЅЮЊгаРэЛЏвђЪНЃЌНЋ![]() ЗжФИгаРэЛЏЕУЁЁ ЁЁЃЎ
ЗжФИгаРэЛЏЕУЁЁ ЁЁЃЎ
ЃЈ2ЃЉМЦЫуЃК2Љ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЙлВьЯТУцЕФБфаЮЙцТЩВЂНтОіЮЪЬтЃЎ
Ђй![]() ЃН
ЃН![]() Љ1ЃЌ
Љ1ЃЌ![]() ЃН
ЃН![]()
![]() ЃЌ
ЃЌ![]() ЃН
ЃН![]() ЃЌЁЃЌШєnЮЊе§ећЪ§ЃЌЧыФуВТЯыЃК
ЃЌЁЃЌШєnЮЊе§ећЪ§ЃЌЧыФуВТЯыЃК![]() ЃНЁЁ ЁЁЃЎ
ЃНЁЁ ЁЁЃЎ
ЂкМЦЫуЃКЃЈ![]() +
+![]() +
+![]() +Ё+
+Ё+![]() ЃЉЁСЃЈ
ЃЉЁСЃЈ![]() +1ЃЉЃЎ
+1ЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉ3+![]() ЃЌ
ЃЌ![]() ЃЛЃЈ2ЃЉ2Љ
ЃЛЃЈ2ЃЉ2Љ![]() ЃЛЃЈ3ЃЉЂй
ЃЛЃЈ3ЃЉЂй![]() Љ
Љ![]() ЃЛЂк2019ЃЎ
ЃЛЂк2019ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЛЅЮЊгаРэЛЏвђЪНЕФЪНзгЬиеїМДПЩаДГі3Љ![]() ЕФгаРэЛЏвђЪНЃЌНЋ
ЕФгаРэЛЏвђЪНЃЌНЋ![]() ЗжзгЁЂЗжФИЭЌЪБГЫ
ЗжзгЁЂЗжФИЭЌЪБГЫ![]() МДПЩЃЛ
МДПЩЃЛ
ЃЈ2ЃЉНЋИУЪНЗжФИгаРэЛЏЃЌШЛКѓЛЏМђМДПЩЃЛ
ЃЈ3ЃЉЂйИљОнЙцТЩМДПЩЧѓГіЃЛ
ЂкИљОнвдЩЯЙцТЩЛЏМђВЂЧѓжЕМДПЩ.
НтЃКЃЈ1ЃЉ3Љ![]() гы3+
гы3+![]() ЛЅЮЊгаРэЛЏвђЪНЃЌНЋ
ЛЅЮЊгаРэЛЏвђЪНЃЌНЋ![]() ЗжФИгаРэЛЏЕУ
ЗжФИгаРэЛЏЕУ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉдЪНЃН2Љ![]() Љ2
Љ2![]() ЃН2Љ
ЃН2Љ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЂй![]() ЃН
ЃН![]() Љ
Љ![]() ЃЛ
ЃЛ
ЂкдЪНЃНЃЈ![]() Љ1+
Љ1+![]() +Ё+
+Ё+![]() ЃЉЃЈ
ЃЉЃЈ![]() +1ЃЉ
+1ЃЉ
ЃНЃЈ![]() Љ1ЃЉЃЈ
Љ1ЃЉЃЈ![]() +1ЃЉ
+1ЃЉ
ЃН2020Љ1
ЃН2019ЃЎ

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИЁОЬтФПЁПЮЊВЮМгбЇаЃЕФЁАЮвАЎЙХЪЋДЪЁБжЊЪЖОКШќЃЌЭѕЯўЫљдкАрМЖзщжЏСЫвЛДЮЙХЪЋДЪжЊЪЖВтЪдЃЌВЂНЋШЋАрЭЌбЇЕФЗжЪ§ЃЈЕУЗжШЁе§ећЪ§ЃЌТњЗжЮЊ100ЗжЃЉНјааЭГМЦЃЌвдЯТЪЧИљОнетДЮВтЪдГЩМЈжЦзїЕФВЛЭъећЕФЦЕТЪЗжВМБэКЭЦЕТЪЗжВМжБЗНЭМЃЎЧыИљОнвдЩЯЦЕТЪЗжВМБэКЭЦЕТЪЗжВМжБЗНЭМЃЌЛиД№ЯТСаЮЪЬтЃК
зщБ№ | Зжзщ | ЦЕЪ§ | ЦЕТЪ |
1 | ЁЁ50ЁмxЃМ60 | 9 | 0.18 |
2 | ЁЁ60ЁмxЃМ70 | a | b |
3 | ЁЁ70ЁмxЃМ80 | 21 | 0.42 |
4 | ЁЁ80ЁмxЃМ90 | m | 0.06 |
5 | ЁЁ90ЁмxЁм100 | 2 | n |
ЃЈ1ЃЉЧѓГіaЁЂbЁЂmЁЂnЕФжЕЃЛ
ЃЈ2ЃЉРЯЪІЫЕЃКЁАЭѕЯўЕФВтЪдГЩМЈЪЧШЋАрЭЌбЇГЩМЈЕФжаЮЛЪ§ЁБЃЌФЧУДЭѕЯўЕФВтЪдГЩМЈдкЪВУДЗЖЮЇФкЃП
ЃЈ3ЃЉШєвЊДгаЁУїЁЂаЁУєЕШМИЮЛГЩМЈгХауЃЈЗжЪ§дк80ЁмxЁм100ЗЖЮЇФкЮЊгХауЃЉЕФЭЌбЇжаЫцЛњбЁШЁСНЮЛВЮМгОКШќЃЌЧыгУЁАСаБэЗЈЁБЛђЁАЪїзДЭМЁБЧѓГіаЁУїЁЂаЁУєЭЌЪББЛбЁжаЕФИХТЪЃЎЃЈзЂЃКМИЮЛЭЌбЇЧыгУAЁЂBЁЂCЁЂDЁБэЪОЃЌЦфжааЁУїЮЊAЃЌаЁУєЮЊBЃЉ