题目内容
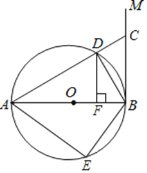
【题目】如图,![]() 是
是![]() 的直径,过点
的直径,过点![]() 作
作![]() 的切线
的切线![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() 与
与![]() 交于点
交于点![]() ,
,![]() 为
为![]() 上一点,且满足
上一点,且满足![]() =
=![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的半径长.
的半径长.
【答案】(1)见详解;(2)![]() .
.
【解析】
(1)先证明![]() ,再证明
,再证明![]() ,最后根据内接四边形对角互补得出
,最后根据内接四边形对角互补得出![]() 即得;
即得;
(2)连接OD,先推出![]() ,再根据相似三角形对应边成比例得出DF=3,最后在
,再根据相似三角形对应边成比例得出DF=3,最后在![]() 中设半径为R,应用勾股定理列出方程求解即得.
中设半径为R,应用勾股定理列出方程求解即得.
(1)∵AB为直径
∴![]()
∴![]()
∵![]() 为
为![]() 的切线
的切线
∴![]()
∴![]() ,
,![]()
∴![]()
∵![]() =
=![]()
∴![]()
∴![]()
∵在![]() 的内接四边形ADBE中,
的内接四边形ADBE中,![]()
∴![]() ,即
,即![]()
∴![]() ,即
,即![]()
(2)如下图:连接OD
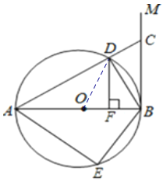
∵DF⊥AB,AB为直径,
∴∠DFO=∠AEB = 90°
∵![]() ,
,![]()
∴∠CBD=∠BAD
∵∠DOF=2∠BAD,![]()
∴∠DOF=∠ABE
∴![]()
∴![]() '
'
∵![]()
∴DF=3
设![]() 的半径为R,则
的半径为R,则![]()
在![]() 中,
中,![]()
即![]()
解得:![]()
所以![]() 的半径长为
的半径长为![]()

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的