Question

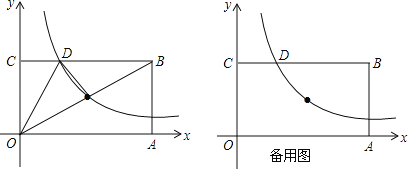
【题目】如图，已知矩形OABC的一个顶点B的坐标是（8，4），反比例函数y=（x＞0）的图象经过OB的中点E，且与边BC交于点D．

（1）求反比例函数的解析式和点D的坐标；

（2）求三角形DOE的面积；

（3）若过点D的直线y=mx+n将矩形OABC的面积分成3：5的两部分，求此直线解析式．

Answer 1

【答案】(1) 反比例函数解析式为y=,点D的坐标为(2,4)；（2）三角形DOE的面积为6；

(3) y=-2x+8或y=x+.

【解析】

(1)根据中心对称求出点E的坐标, 再代入反比例函数解析式求出k, 然后根据点D的纵坐标与点B的纵坐标相等代入求解即可得到点D的坐标;

(2) 根据点D的坐标求出BD的长, 再由点E是OB的中点可知,由此可得出结论;

(3) 设直线与x轴的交点为F, 根据点D的坐标求出CD, 再根据梯形的面积分两种情况求出OF的长, 然后写出点F的坐标, 再利用待定系数法求一次函数的解析式即可.

解：(1)矩形OABC的顶点B的坐标是(8,4), E是矩形ABCD 的对称中心,

点E的坐标为(4,2),代入反比例函数解析式得=2, 解得k=8,

反比例函数解析式为y=

点D在边BC上,点D的纵坐标为4,

y=4时, x=2,

点D的坐标为(2,4);

(2)D的坐标为(2,4),B(8,4),

BD=6, OC=4.

点E是OB的中点,

==6

(3) 如图,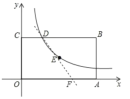

设直线与x轴的交点为F,矩形OABC的面积=84=32,

矩形OABC的面积分成3:5的两部分,

梯形OFDC的面积为=12,或者=20

点D的坐标为(2,4),

若(2+OF)4=12,

解得OF=4,此时点F的坐标为(4,0),

若 (2+OF)4=20,

解得OF=8, 此时点F的坐标为(8,0),与A点重合，

当D(2,4),F(4,0)时,可得函数解析式为y=-2x+8

当D(2,4),F(8,0)时，可得函数解析式为y=x+

综上所述,直线的解析式为y=-2x+8或y=x+.