题目内容
如图,在直角坐标系内有等腰三角形OAB,O为原点,顶点A的坐标为(3 ,3),
,3),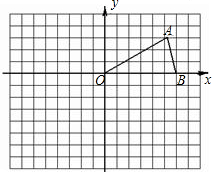 B的坐标为(6,0).
B的坐标为(6,0).
(1)在坐标系中作△OAB关于y轴对称的图形△OA′B′;
(2)将△OAB绕点O按顺时针方向旋转90°得△OCD.画出△OCD,并写出点C的坐标;
(3)猜测∠AOB的度数,并说明理由.
 解:(1)图形△OA′B′正确
解:(1)图形△OA′B′正确(2)画出△OCD正确;
点C(3,-3
 )
)(3)猜测∠AOB的度数为30°
理由:过A作AE⊥x轴于E,取AO中点为F,连接EF,
则可知Rt△AEO中,
∵等腰三角形OAB,OB=OA=6,
∴斜边AO=6,直角边AE=3,AF=AE=3,
所以△AEF是等边三角形,∠FAE=60°,所以∠AOB=30°
分析:(1)先求出三角形的三个顶点O、A、B关于y轴对称的点O、A′、B′的坐标,再描点画出△OA′B′即可;
(2)先求出△OAB绕点O旋转得到的△OCD中CD两点的坐标,再描点画出△OCD即可;
(3)先过A作AE⊥x轴于E,取AO中点为F,推得△AEF是等边三角形,从而求出∠AOB的度数.
点评:作旋转后的图形的依据是旋转的性质,基本作法是①先确定图形的关键点;②利用旋转性质作出关键点的对应点;③按原图形中的方式顺次连接对应点.要注意旋转中心,旋转方向和角度.

练习册系列答案
相关题目
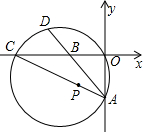 AB的延长线交于点D,弧CD=弧AO,如果AB=10,AO>BO,且AO、BO是x的二次方程x2+kx+48=0的两个根.
AB的延长线交于点D,弧CD=弧AO,如果AB=10,AO>BO,且AO、BO是x的二次方程x2+kx+48=0的两个根.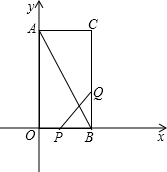
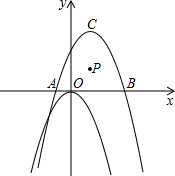 (2007•西城区二模)如图,在直角坐标系内有点P(1,1)、点C(1,3)和二次函数y=-x2.
(2007•西城区二模)如图,在直角坐标系内有点P(1,1)、点C(1,3)和二次函数y=-x2.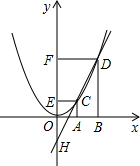 如图,在直角坐标系内,O为坐标原点,点A的坐标为(1,0),点B在x轴上且在点A的右端,OA=AB,分别过点A、B作x轴的垂线,与二次函数y=x2的图象交于C、D两点,分别过点C、D作y轴的垂线,交y轴于点E、F,直线CD交y轴于点H.
如图,在直角坐标系内,O为坐标原点,点A的坐标为(1,0),点B在x轴上且在点A的右端,OA=AB,分别过点A、B作x轴的垂线,与二次函数y=x2的图象交于C、D两点,分别过点C、D作y轴的垂线,交y轴于点E、F,直线CD交y轴于点H.