题目内容
【题目】如图,D是给定△ABC边BC所在直线上一动点,E是线段AD上一点,DE=2AE,连接BE,CE,点D从B的左边开始沿着BC方向运动,则△BCE的面积变换情况是( )
A.逐渐变大
B.逐渐变小
C.先变小后变大
D.始终不变
【答案】D
【解析】解:如图,过点E作EF⊥BC于F,过点A作AG⊥BC于G,
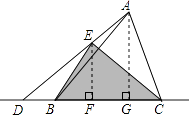
则EF∥AG,
所以,△ADG∽△EDF,
所以, ![]() =
= ![]() ,
,
∵DE=2AE,
∴AD=DE+AE=3AE,
∴ ![]() =
= ![]() ,
,
∴EF= ![]() AG,
AG,
∴△BCE的面积= ![]() BCEF=
BCEF= ![]() BC
BC ![]() AG=
AG= ![]() ×
× ![]() BCAG=
BCAG= ![]() S△ABC,
S△ABC,
∴△BCE的面积始终不变.
故答案为:D.
观察图形,△BCE和△ABC由公共边BC,只需找到这两个三角形BC边上的高之间的关系,即可求解。过点E作EF⊥BC于F,过点A作AG⊥BC于G,先证明△ADG∽△EDF,得到两条高之间的数量关系,再求出两三角形之间的面积关系即可。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】下表是小颖往表姐家打长途电话的收费记录:
通话时间x(分钟) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
电话费y(元) | 3 | 3 | 3 | 3.6 | 4.2 | 4.8 | 5.4 |
(1)上表的两个变量中, 是自变量, 是因变量;
(2)写出y与x之间的关系式;
(3)若小颖的通话时间是15分钟,则需要付多少电话费?
(4)若小颖有24元钱,则她最多能打多少分钟电话?