题目内容
【题目】如图,已知直角坐标系中一条圆弧经过正方形网格的格点A,B,C.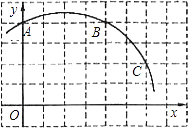
(1)用直尺画出该圆弧所在圆的圆心M的位置;
(2)若A点的坐标为(0,4),D点的坐标为(7,0),试验证点D是否在经过点A,B,C的抛物线上;
(3)在(2)的条件下,求证:直线CD是⊙M的切线.
【答案】
(1)解:如图1,点M即为所求
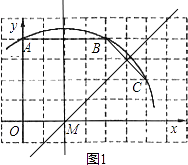
(2)解:由A(0,4),可得小正方形的边长为1,从而B(4,4)、C(6,2)
设经过点A、B、C的抛物线的解析式为y=ax2+bx+4
依题意 ![]() ,解得
,解得 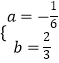
所以经过点A、B、C的抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+4
x+4
把点D(7,0)的横坐标x=7代入上述解析式,得 ![]()
所以点D不在经过A、B、C的抛物线上;
(3)证明:如图,设过C点与x轴垂直的直线与x轴的交点为E,连接MC,作直线CD
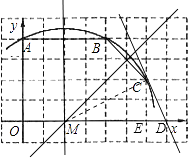
∴CE=2,ME=4,ED=1,MD=5
在Rt△CEM中,∠CEM=90°
∴MC2=ME2+CE2=42+22=20
在Rt△CED中,∠CED=90°
∴CD2=ED2+CE2=12+22=5
∴MD2=MC2+CD2
∴∠MCD=90°
∵MC为半径
∴直线CD是⊙M的切线
【解析】(1)根据垂径定理的知识解答此题。
(2)观察图形,由点A的坐标,得到点B、C的坐标,用待定系数法求出抛物线的解析式,将x=7代入即可得出结果。
(3)要证直线CD是⊙M的切线.就需证明∠MCD=90°,运用勾股定理先分别求出MC2、CD2、MD2,再用勾股定理的逆定理去判定∠MCD是否为直角即可。
【考点精析】关于本题考查的垂径定理和确定圆的条件,需要了解垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;不在同一直线上的三点确定一个圆才能得出正确答案.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】铁一课间餐种类繁多,深受学生喜爱.这天饭堂在课间的出品有鸡腿、薯饼、鱼丸和鸡柳.某同学就九年级学生对课间餐各类食物的喜爱程度做了抽样调查,制成表格如下:
课间餐种类 | 人类 | 百分比 |
鸡腿 | 150 | 60% |
薯饼 | 30 | a |
鱼丸 | b | 12% |
鸡柳 | 40 | c |
(1)样本容量是 , a= , b= , c= .
(2)若小王和小李商议着一起去买课间餐,若他们对以上四种口味的课间餐喜爱程度相同.请你帮他们算一算他们买了相同课间餐的概率.