Question

【题目】为方便市民低碳生活绿色出行，市政府计划改造如图所示的人行天桥：天桥的高是10米，原坡面倾斜角∠CAB=45°．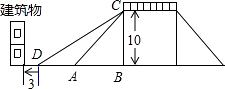

（1）若新坡面倾斜角∠CDB=28°，则新坡面的长CD长是多少？（精确到0.1米）
（2）若新坡角顶点D前留3米的人行道，要使离原坡角顶点A处10米的建筑物不拆除，新坡面的倾斜角∠CDB度数的最小值是多少？（精确到1°）

Answer 1

【答案】
（1）解：在Rt△BCD中，

∵BC=10，∠CDB=28°，

∴CD= = ≈21.3（米），

答：新坡面的长为21.3米

（2）解：∵∠CAB=45°，

∴AB=CB=10，

又建筑物离原坡角顶点A处10米，即建筑物离天桥底点B的距离为20米，

当DB取最大值时，∠CDB达最小值，

要使建筑物不被拆掉DB的最大值为20﹣3=17，

则tan∠CDB= = ≈0.588，

∴∠CDB≈31°．

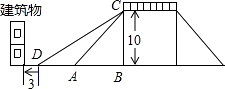
答：若新坡角顶点D前留3米的人行道，要使离原坡角顶点A处10米的建筑物不拆除，新坡面的倾斜角的最小值是31°

【解析】（1）在Rt△BCD中，已知BC、∠CDB的度数，利用解直角三角形就可以求出CD的长。
（2）已知建筑物距A10米，由已知可证得△ACB是等腰直角三角形，得出AB=10,由此可求得DB的最大值，当DB取最大值时，∠CDB达最小值，然后在Rt△DBC中利用解直角三角形就可以求出∠CDB的度数。
【考点精析】本题主要考查了解直角三角形和关于坡度坡角问题的相关知识点，需要掌握解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)；坡面的铅直高度h和水平宽度l的比叫做坡度(坡比)．用字母i表示，即i=h/l．把坡面与水平面的夹角记作A(叫做坡角)，那么i=h/l=tanA才能正确解答此题．