题目内容
如图,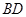 为⊙
为⊙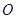 的直径,点
的直径,点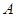 是弧
是弧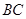 的中点,
的中点,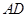 交
交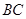 于
于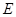 点,
点,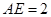 ,
,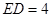 .
.
(1)求证: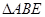 ∽
∽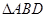 ;
;
(2) 求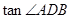 的值;
的值; 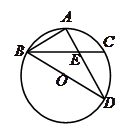
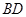 为⊙
为⊙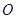 的直径,点
的直径,点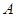 是弧
是弧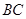 的中点,
的中点,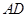 交
交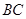 于
于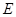 点,
点,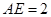 ,
,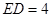 .
. (1)求证:
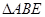 ∽
∽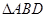 ;
;(2) 求
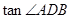 的值;
的值; 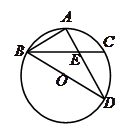
解(1)∵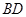 为⊙
为⊙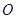 的直径,∴∠A=
的直径,∴∠A=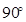
即∠BAE=∠BAE
又∵点A是弧BC的中点, ∴∠ABC=∠D.
∴△ABE∽△ABD.
(2)∵△ABE∽△ABD,∴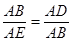
∴AB2=2×6=12. ∴AB=2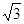 .
.
∴在Rt△ADB中,tan∠ADB=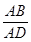 =
=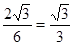 .
.
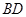 为⊙
为⊙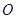 的直径,∴∠A=
的直径,∴∠A=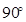
即∠BAE=∠BAE
又∵点A是弧BC的中点, ∴∠ABC=∠D.
∴△ABE∽△ABD.
(2)∵△ABE∽△ABD,∴
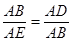
∴AB2=2×6=12. ∴AB=2
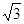 .
. ∴在Rt△ADB中,tan∠ADB=
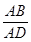 =
=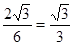 .
. (1)由同弧或等弧所对的圆周角相等可得∠ABC=∠D,再由公共角∠BAE即得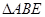 ∽
∽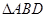 ;
;
(2)根据相似三角形的对应边成比例可求出AB的长,根据直径所对的圆周角是直角即可知∠BAD是直角,从而可求得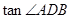 。
。
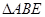 ∽
∽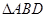 ;
;(2)根据相似三角形的对应边成比例可求出AB的长,根据直径所对的圆周角是直角即可知∠BAD是直角,从而可求得
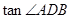 。
。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
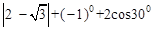
 ;
;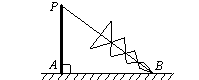
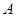 ,用测角仪测出看塔顶
,用测角仪测出看塔顶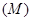 的仰角
的仰角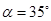 ,在
,在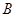 ,测出看塔顶
,测出看塔顶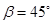 ,然后用皮尺量出
,然后用皮尺量出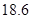 m,自身的高度为
m,自身的高度为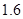 m.请你利用上述数据帮助小华计算出塔的高度(
m.请你利用上述数据帮助小华计算出塔的高度(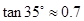 ,结果保留整数).
,结果保留整数).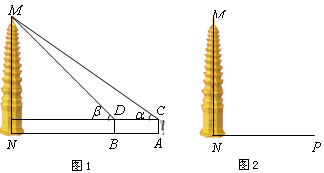
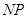 的长为
的长为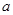 m(如图2),你能否利用这一数据设计一个测量方案?如果能,
m(如图2),你能否利用这一数据设计一个测量方案?如果能,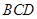 中,∠
中,∠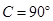 ,∠
,∠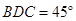 ,利用此等腰直角三角形你能求出
,利用此等腰直角三角形你能求出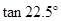 的值吗?
的值吗?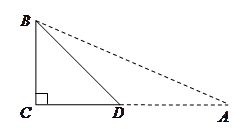
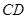 到点
到点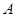 ,使
,使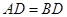 ,连结
,连结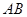 .
.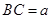 (
(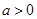 ).
). .
.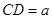 ,
,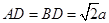 .
.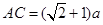 .
.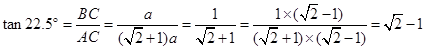 .
.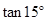 的值;
的值;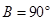 ,∠
,∠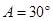 ,
,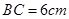 ;图2中,∠
;图2中,∠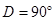 ,∠
,∠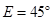 ,
,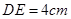 .图3是小刘所做的一个实验:他将△
.图3是小刘所做的一个实验:他将△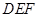 的直角边
的直角边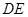 与△
与△ 的斜边
的斜边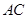 重合在一起,并将△
重合在一起,并将△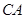 方向移动.在移动过程中,
方向移动.在移动过程中,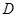 、
、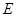 两点始终在
两点始终在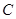 重合).
重合).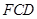 的度数逐渐__________.(填“不变”、“变大”、“变小”)
的度数逐渐__________.(填“不变”、“变大”、“变小”)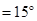 ?如果存在,求出
?如果存在,求出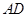 的长度;如果不存在,请说明理由.
的长度;如果不存在,请说明理由.
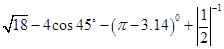 .
.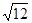 +
+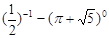 -2tan600
-2tan600