题目内容
 如图,在等腰△ABC中,AB=AC,D为BC边上的一个动点,E、F分别是AC、AB边上的点,且DF∥AC、CE=DE.
如图,在等腰△ABC中,AB=AC,D为BC边上的一个动点,E、F分别是AC、AB边上的点,且DF∥AC、CE=DE.
(1)证明:四边形DEAF是平行四边形;
(2)当点D在BC边上运动时,(DF∥AC、CE=DE保持不变)那么是否存在点D,使四边形AFDE为菱形(不再增添辅助线),并请证明你的结论.
(这样改动的目的是使学生明白当点D运动时,E、F也在运动.)
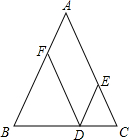 证明:(1)∵DF∥AC,
证明:(1)∵DF∥AC,∴∠FDC=∠C.
又∵AB=AC,CE=DE,
∴∠B=∠C,∠EDC=∠C.
∴∠B=∠EDC.
∴DE∥AB.
又∵DF∥AC,
∴四边形DEAF是平行四边形.
(2)当点D运动到BC的中点处时,四边形DEAF是菱形;
由(1)可知:∠B=∠C,
∠EDB=∠FDC,
又∵BC=CD,
∴△BDE≌△CDF.
∴DE=DF且四边形DEAF是平行四边形.
∴四边形DEAF是菱形.
分析:(1)可通过证明AF∥DE来得出结论,根据两组相等边,可得出∠B=∠C,∠EDC=∠C,那么∠EDC=∠B,由此可得出AF∥DE,再根据DF∥AC即可得出本题所求的结论.
(2)存在这样的D点,因为首先AFDE是个平行四边形,要使其成为菱形,那么AE=DE=CE,DE就是三角形ABC的中位线,那么此时D是BC的中点.
点评:本题主要考查了等腰三角形的性质,平行四边形和菱形的判定等知识点.

练习册系列答案
相关题目
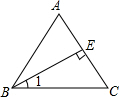 如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )
如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )| A、∠1=∠A | ||
B、∠1=
| ||
| C、∠1=2∠A | ||
| D、无法确定 |
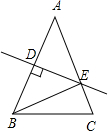 如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=
如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=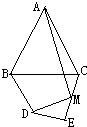 24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.
24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.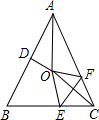 (2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是
(2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是
如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是