Question

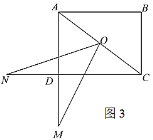
【题目】如图，△ABC≌△DBE,点D在边AC上,BC与DE交于点P．已知, ,,.

(1)求∠CBE的度数．

(2)求△CDP与△BEP的周长和．

Answer 1

【答案】（1）66°；（2）15.5．

【解析】

（1）根据全等三角形的性质得到∠ABC=∠DBE，计算即可；

（2）根据全等三角形的性质求出BE、DE，根据三角形的周长公式计算即可．

（1）∵△ABC≌△DBE，

∴∠ABC=∠DBE．

∴∠ABC-∠DBC =∠DBE-∠DBC，即∠ABD=∠CBE．

∵∠ABD+∠DBC+∠CBE =∠ABE，

∴∠CBE=(∠ABE-∠DBC)=×(162°-30°)=66°．

（2）∵△ABC≌△DBE，

∴DE=AC=AD+DC=5，BE=BC=4，

∴△CDP与△BEP的周长和=DC+DP+PC+BP+PE+BE=DC+DE+BC+BE=2.5+5+4+4=15.5．