题目内容
(本小题满分14分)
如图,已知抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3)。设抛物线的顶点为D,求解下列问题: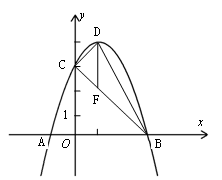
【小题1】(1)求抛物线的解析式和D点的坐标;
【小题2】(2)过点D作DF∥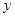 轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
【小题3】(3)能否在抛物线上找到一点Q,使△BDQ为直角三角形?若能找到,试写出Q点的坐标;若不能,请说明理由。

【小题1】解:(1)设抛物线的解析式为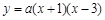
把(0,3)代入,解得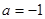 ,
,
解析式为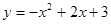 -----------------------2分
-----------------------2分
则点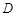 的坐标为(1,4)-----------------------2分
的坐标为(1,4)-----------------------2分
【小题2】(2)设直线BC的解析式为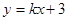 ,把B(3,0)代入,
,把B(3,0)代入,
解得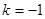 ,所以
,所以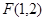
∴DF= -----------------------2分
-----------------------2分
△BCD的面积= --------------2分
--------------2分
【小题3】(3)①点 即在抛物线上,CD=
即在抛物线上,CD= ,BC=
,BC=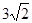 ,
,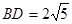 。
。
∵ ,
,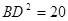 ,∴
,∴ ∴
∴ ,
,
这时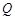 与
与 点重合点
点重合点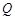 坐标为
坐标为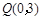 ----------------------------------2分
----------------------------------2分
②如图(4),若 为
为 ,作QF⊥
,作QF⊥ 轴于
轴于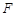 ,
,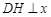 轴于
轴于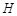
可证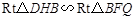
有
则点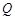 坐标
坐标
即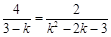
化简为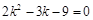
即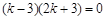
解之为 或
或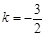
由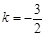 得
得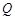 坐标:
坐标: ----------2分
----------2分
③若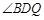 为
为
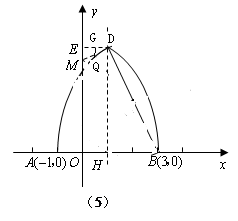
如图(5),延长 交
交 轴于
轴于 ,
,
作 轴于
轴于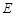 ,
,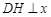 轴于
轴于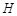
可证明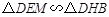
即
则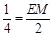
得 ,
,
解法(1)过Q作QG∥ 轴交DE于点G,∴
轴交DE于点G,∴
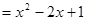 ,
, ,
,
∴ ,
, 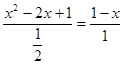 ,解得
,解得 (舍去)
(舍去) ,
,
代入解得 ,
,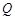 为
为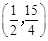
解法(2)点 的坐标为
的坐标为
 所在的直线方程为
所在的直线方程为
则 与
与 的解为
的解为 ,得交点坐标
,得交点坐标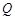 为
为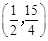 &middo
&middo
解析

练习册系列答案
相关题目
 如图13,二次函数
如图13,二次函数 与y轴交于点C(0,
与y轴交于点C(0, ), 与x轴交于点A、 B,点A的坐标为(2,0).
), 与x轴交于点A、 B,点A的坐标为(2,0).
 与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为(
与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为( ,0).问:是否存在这样的直线
,0).问:是否存在这样的直线 与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线
与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线 与抛物线交于点B、C.
与抛物线交于点B、C.
 与
与 的面积。
的面积。 时,
时, 是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.
是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.