题目内容
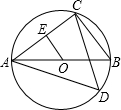 (2013•江北区模拟)如图,AB是⊙O的直径,点C在⊙O上,AB=5,BC=3,
(2013•江北区模拟)如图,AB是⊙O的直径,点C在⊙O上,AB=5,BC=3,(1)若OE⊥AC于点E,求OE的长;
(2)若点D为优弧ABC上一点,求tan∠ADC的值.
分析:(1)求出∠ACB=90°,AC=4,由垂径定理可得EA=2,在Rt△AEO中根据勾股定理求出即可.
(2)求出∠D=∠B,求出∠B的正切值即可.
(2)求出∠D=∠B,求出∠B的正切值即可.
解答: (1)解:∵AB是⊙O直径,
(1)解:∵AB是⊙O直径,
∴∠ACB=90°,
∵AB=5,BC=3,
∴AC=4,
又∵OE⊥AC,
∴由垂径定理可得EA=2,
在Rt△AEO中,OE=
=
.
(2)∵∠B,∠D是弧AC所对圆周角,
∴∠B=∠D,
∴tan∠D=tan∠B=
.
 (1)解:∵AB是⊙O直径,
(1)解:∵AB是⊙O直径,∴∠ACB=90°,
∵AB=5,BC=3,
∴AC=4,
又∵OE⊥AC,
∴由垂径定理可得EA=2,
在Rt△AEO中,OE=
| OA2-OE2 |
| 3 |
| 2 |
(2)∵∠B,∠D是弧AC所对圆周角,
∴∠B=∠D,
∴tan∠D=tan∠B=
| 4 |
| 3 |
点评:本题考查了勾股定理,垂径定理,圆周角定理,锐角三角函数的定义等知识点的应用,主要考查学生的推理能力,第一小题也可以根据三角形的中位线求出OE=
BC,代入求出OE.
| 1 |
| 2 |

练习册系列答案
相关题目
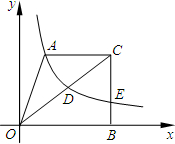 (2013•江北区模拟)如图,在平面直角坐标系中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线y=
(2013•江北区模拟)如图,在平面直角坐标系中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线y=
 (2013•江北区模拟)在平面直角坐标系中,O是坐标原点,直角梯形AOCD的顶点A的坐标为(0,
(2013•江北区模拟)在平面直角坐标系中,O是坐标原点,直角梯形AOCD的顶点A的坐标为(0,