题目内容
 (2013•江北区模拟)在平面直角坐标系中,O是坐标原点,直角梯形AOCD的顶点A的坐标为(0,
(2013•江北区模拟)在平面直角坐标系中,O是坐标原点,直角梯形AOCD的顶点A的坐标为(0,| 3 |
| 3 |
(1)求抛物线的解析式及点P的坐标;
(2)在y轴右侧的抛物线上是否存在点Q,使以Q为圆心的圆同时与y轴、直线OP相切?若存在,请求出满足条件的点Q的坐标;若不存在,请说明理由;
(3)点M为线段OP上一动点(不与O点重合),过点O、M、D的圆与y轴的正半轴交于点N.求证:OM+ON为定值.
(4)在y轴上找一点H,使∠PHD最大.试求出点H的坐标.
分析:(1)因为抛物线的顶点D的坐标为(1,
),所以可设设抛物线的解析式为y=a(x-1)2+
,又因为函数图象过原点,所以把(0,0)代入求出a的值即可求出抛物线的解析式,设y=0,则可求出抛物线和x轴的交点坐标,进而求出点P的坐标;
(2)在y轴右侧的抛物线上存在点Q,使以Q为圆心的圆同时与y轴、直线OP相切,此题要分两种情况讨论:①若⊙Q在直线OP上方②若⊙Q在直线OP下方,再分别求出符合题意的Q点的坐标即可;
(3)由圆周角定理可证明MD=ND,进而证明△NAD≌△MPD(HL),由全等三角形的性质可得MP=AN,所以OM+ON=OP-MP+OA+AN=OP+OA=2OA=
,则OM+ON=2
,即OM+ON为定值;
(4)作过P、D两点且与y轴相切于点H的圆S,则由圆周角大于圆外角可知,∠PHD最大,S(x,y),则由HS=SD=SP,继而求出点H坐标.
| 3 |
| 3 |
(2)在y轴右侧的抛物线上存在点Q,使以Q为圆心的圆同时与y轴、直线OP相切,此题要分两种情况讨论:①若⊙Q在直线OP上方②若⊙Q在直线OP下方,再分别求出符合题意的Q点的坐标即可;
(3)由圆周角定理可证明MD=ND,进而证明△NAD≌△MPD(HL),由全等三角形的性质可得MP=AN,所以OM+ON=OP-MP+OA+AN=OP+OA=2OA=
| 3 |
| 3 |
(4)作过P、D两点且与y轴相切于点H的圆S,则由圆周角大于圆外角可知,∠PHD最大,S(x,y),则由HS=SD=SP,继而求出点H坐标.
解答: 解:(1)∵抛物线的顶点D的坐标为(1,
解:(1)∵抛物线的顶点D的坐标为(1,
),
∴设抛物线的解析式为y=a(x-1)2+
,
将(0,0)代入,得a+
=0,a=-
,
∴抛物线的解析式为y=-
(x-1)2+
,
即 y=-
x2+2
x,
设y=0,则x=0或2,
∴点C的坐标为(0,2),
∵点P为CD的中点,
∴P(
,
);
(2)在y轴右侧的抛物线上存在点Q,使以Q为圆心的圆同时与y轴、直线OP相切,
理由如下:
①若⊙Q在直线OP上方,则Q与D点重合,此时Q1(1,
);
②若⊙Q在直线OP下方,与y轴、直线OP切于E、F,
则QE=QF,QE⊥y轴,QF⊥OP,
∴OQ平分∠EOF,
∵∠EOF=120°,
∴∠FOQ=60°,
∵∠POC=30°,则∠QOC=30°,
设Q(m,-
m),则-
m=-
m2+2
m,
解得m1=0(舍去),m2=
,
∴Q2(
,-
);
(3)证明:∵在过点O、M、D的圆中,有∠MOD=∠NOD,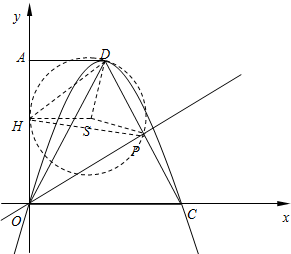
∴
=
,
∴MD=ND,
易得OD平分∠AOP,DA⊥y轴,DP⊥OP,
∴DA=DP,
可证得△NAD≌△MPD(HL),
∴MP=AN,
∴OM+ON=OP-MP+OA+AN=OP+OA=2OA=
,
则OM+ON=2
,即OM+ON为定值;
(4)作过P、D两点且与y轴相切于点H的圆S,
则由圆周角大于圆外角可知,∠PHD最大.
设S(x,y),则由HS=SD=SP,
可得,y=2
±6,
∵0<y<
,
∴H(0,2
-6).
 解:(1)∵抛物线的顶点D的坐标为(1,
解:(1)∵抛物线的顶点D的坐标为(1,| 3 |
∴设抛物线的解析式为y=a(x-1)2+
| 3 |
将(0,0)代入,得a+
| 3 |
| 3 |
∴抛物线的解析式为y=-
| 3 |
| 3 |
即 y=-
| 3 |
| 3 |
设y=0,则x=0或2,
∴点C的坐标为(0,2),
∵点P为CD的中点,
∴P(
| 3 |
| 2 |
| ||
| 2 |
(2)在y轴右侧的抛物线上存在点Q,使以Q为圆心的圆同时与y轴、直线OP相切,
理由如下:
①若⊙Q在直线OP上方,则Q与D点重合,此时Q1(1,
| 3 |
②若⊙Q在直线OP下方,与y轴、直线OP切于E、F,
则QE=QF,QE⊥y轴,QF⊥OP,
∴OQ平分∠EOF,
∵∠EOF=120°,
∴∠FOQ=60°,
∵∠POC=30°,则∠QOC=30°,
设Q(m,-
| ||
| 3 |
| ||
| 3 |
| 3 |
| 3 |
解得m1=0(舍去),m2=
| 7 |
| 3 |
∴Q2(
| 7 |
| 3 |
7
| ||
| 9 |
(3)证明:∵在过点O、M、D的圆中,有∠MOD=∠NOD,

∴
 |
| MD |
 |
| ND |
∴MD=ND,
易得OD平分∠AOP,DA⊥y轴,DP⊥OP,
∴DA=DP,
可证得△NAD≌△MPD(HL),
∴MP=AN,
∴OM+ON=OP-MP+OA+AN=OP+OA=2OA=
| 3 |
则OM+ON=2
| 3 |
(4)作过P、D两点且与y轴相切于点H的圆S,
则由圆周角大于圆外角可知,∠PHD最大.
设S(x,y),则由HS=SD=SP,
可得,y=2
| 3 |
∵0<y<
| 3 |
∴H(0,2
| 3 |
点评:本题着重考查了待定系数法求二次函数解析式、中点坐标公式、全等三角形的判定和性质、圆周角定理的运用、角平分线的性质以及考查学生分类讨论,数形结合的数学思想方法,题目的综合性强,难度大,对学生的综合解题能力要求很高.

练习册系列答案
相关题目
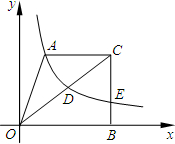 (2013•江北区模拟)如图,在平面直角坐标系中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线y=
(2013•江北区模拟)如图,在平面直角坐标系中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线y=