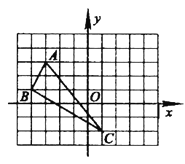
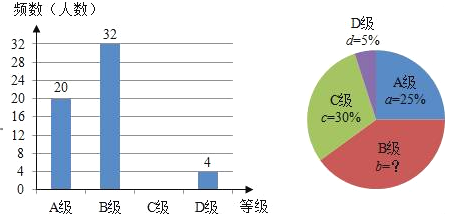
��Ŀ����
����Ŀ���Ķ����ϣ�������⣺
���ǿ������ý��Ԫһ�η�����Ĵ�����Ԫ��������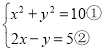 �Ķ�Ԫ���η����飬ʵ���ǽ���Ԫ���η�����ת��ΪһԪһ�η��̻�һԪ���η�������⣮��ⷨ���£�
�Ķ�Ԫ���η����飬ʵ���ǽ���Ԫ���η�����ת��ΪһԪһ�η��̻�һԪ���η�������⣮��ⷨ���£�
�⣺�ɢڵã�y=2x-5 ��
���۴���ٵã�x2+��2x-5��2=10
�����ã�x2-4x+3=0�����x1=1��x2=3
��x1=1��x2=3����۵�y1=1��2-5=-3��y2=2��3-5=1
��ԭ������Ľ�Ϊ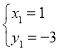 ��
��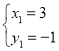 ��
��
��1�������ô�����Ԫ�����Ԫ���η����飺 ��
��
��2������x��y�Ķ�Ԫ���η�����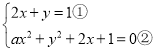 �����鲻ͬ��ʵ���⣬��ʵ��a��ȡ�ŷ�Χ��
�����鲻ͬ��ʵ���⣬��ʵ��a��ȡ�ŷ�Χ��
���𰸡�(1) ![]() ��(2) a��-
��(2) a��-![]() ��a��-4��
��a��-4��
��������
�����������1������ȥһ��δ֪���ٽ������һ��δ֪���Ĵη��̣�����ý������һ���ϼķ����м��ɣ�
��2������ȥһ��δ֪�����õ�������һ��δ֪����һԪ���η��̣�����һԪ���η��̸����б�ʽ��ɣ�
�����������1���ɢٵã�y=2x-3�ۣ�
�Ѣ۴���ڵã���2x-3��2-4x2+6x-3=0��
�����ģ�6x=6��
���x=1��
��x=1����۵ã�y=-1��
��ԭ������Ľ�Ϊ![]() ��
��
��2���ɢٵã�y=1-2x�ۣ�
�Ѣ۴���ڵã�ax2+��1-2x��2+2x+1=0��
�������a+4��x2-2x+2=0��
������ã�4-4��2����a+4����0��
���a��-![]() ��
��
��a+4��0��
��a��-4��
��a��-![]() ��a��-4��
��a��-4��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�