ÌâÄżÄÚÈĘ
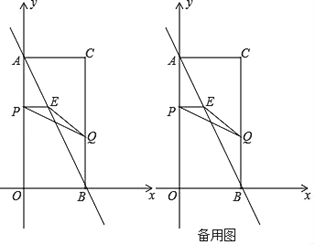
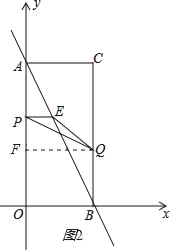
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹÒŃÖȘŸŰĐÎAOBC”Ķ„”ăC”ÄŚű±êÊÇŁš2ŁŹ4Ł©ŁŹ¶Ż”ăPŽÓ”ăAłö·ąŁŹŃŰÏ߶ÎAOÏòÖŐ”ăOÔ˶ŻŁŹÍŹÊ±¶Ż”ăQŽÓ”ăBłö·ąŁŹŃŰÏ߶ÎBCÏòÖŐ”ăCÔ˶ŻŁź”ăPĄąQ”ÄÔ˶ŻËٶȟùÎȘĂżĂë1žö”„λŁŹÉèÔ˶ŻÊ±ŒäÎȘtĂ룏čę”ăPŚśPEĄÍAOœ»ABÓÚ”ăEŁź
Łš1Ł©ÇóÖ±ÏßAB”ÄœâÎöÊœŁ»
Łš2Ł©ÔÚ¶Ż”ăPĄąQÔ˶Ż”ÄčęłÌÖĐŁŹÒÔBĄąQĄąEÎȘ¶„”ă”ÄÈęœÇĐÎÊÇÖ±œÇÈęœÇĐÎŁŹÖ±°ŽĐŽłöt”ÄÖ”Ł»
Łš3Ł©ÉèĄśPEQ”ÄĂæ»ęÎȘSŁŹÇóSÓëʱŒät”ÄșŻÊęčŰÏ”ŁŹČąÖžłöŚÔ±äÁżt”ÄÈĄÖ”·¶Î§Łź
ĄŸŽđ°žĄżŁš1Ł©yŁœ©2x+4Łš2Ł©2»ò![]() Łš3Ł©SŁœ
Łš3Ł©SŁœ![]() t2©tŁš2ŁŒtĄÜ4Ł©
t2©tŁš2ŁŒtĄÜ4Ł©
ĄŸœâÎöĄż
Łš1Ł©ÒÀŸĘŽę¶šÏ”Êę·šŒŽżÉÇó”ĂŁ»
Łš2Ł©žùŸĘÖ±œÇÈęœÇĐΔÄĐÔÖÊœâŽđŒŽżÉŁ»
Łš3Ł©ÓĐÁœÖÖÇéżöŁș”±0ŁŒtŁŒ2ʱŁŹPFŁœ4©2tŁŹ”±2ŁŒtĄÜ4ʱŁŹPFŁœ2t©4ŁŹÈ»șóžùŸĘĂæ»ęč«ÊœŒŽżÉÇó”ĂŁ»
Łš1Ł©ĄßCŁš2ŁŹ4Ł©ŁŹ
ĄàAŁš0ŁŹ4Ł©ŁŹBŁš2ŁŹ0Ł©ŁŹ
ÉèÖ±ÏßAB”ÄœâÎöÊœÎȘyŁœkx+bŁŹ
Ąà![]() ŁŹ
ŁŹ
œâ”Ă![]() ŁŹ
ŁŹ
ĄàÖ±ÏßAB”ÄœâÎöÊœÎȘyŁœ©2x+4Łź
Łš2Ł©”±ÒÔBĄąQĄąEÎȘ¶„”ă”ÄÈęœÇĐÎÊÇÖ±œÇÈęœÇĐÎʱŁŹPĄąEĄąQčČÏߣŹŽËʱtŁœ2ŁŹ
”±ÒÔBĄąQĄąEÎȘ¶„”ă”ÄÈęœÇĐÎÊÇÖ±œÇÈęœÇĐÎʱŁŹEQĄÍBEʱŁŹŽËʱtŁœ![]() Ł»
Ł»
Łš3Ł©ÈçÍŒ2ŁŹčę”ăQŚśQFĄÍyÖáÓÚFŁŹ
ĄßPEĄÎOBŁŹ
Ąà![]() ŁŹ
ŁŹ
ĄßAPŁœBQŁœtŁŹĄàPEŁœ![]() tŁŹAFŁœCQŁœ4©tŁŹ
tŁŹAFŁœCQŁœ4©tŁŹ
”±0ŁŒtŁŒ2ʱŁŹPFŁœ4©2tŁŹ
ĄàSŁœ![]() PEPFŁœ
PEPFŁœ![]() ĄÁ
ĄÁ![]() tŁš4©2tŁ©Łœt©
tŁš4©2tŁ©Łœt©![]() t2ŁŹ
t2ŁŹ
ŒŽSŁœ©![]() t2+tŁš0ŁŒtŁŒ2Ł©ŁŹ
t2+tŁš0ŁŒtŁŒ2Ł©ŁŹ
”±2ŁŒtĄÜ4ʱŁŹPFŁœ2t©4ŁŹ
ĄàSŁœ![]() PEPFŁœ
PEPFŁœ![]() ĄÁ
ĄÁ![]() tŁš2t©4Ł©Łœ/span>
tŁš2t©4Ł©Łœ/span>![]() t2©tŁš2ŁŒtĄÜ4Ł©Łź
t2©tŁš2ŁŒtĄÜ4Ł©Łź

 ŚÛșÏŚÔČâÏ”ÁĐŽđ°ž
ŚÛșÏŚÔČâÏ”ÁЎ𰞥ŸÌâÄżĄżŃĆ°Č”ŰŐđ·ąÉúșóŁŹÈ«čúÈËĂńżčŐđŸÈÔÖŁŹÖÚÖŸłÉłÇŁŹÖ””ŰŐđ·ąÉúÒ»ÖÜÄêÖźŒÊŁŹÄł”ŰŐțžźÓÖłïŒŻÁËÖŰœšŒÒÔ°”ıŰĐèÎïŚÊ120¶ÖŽòËăÔËÍùÔÖÇűŁŹÏÖÓĐŒŚĄąÒÒĄą±ûÈęÖÖł”ĐÍč©ŃĄÔńŁŹĂżÁŸł””ÄÔËÔŰÄÜÁŠșÍÔË·ŃÈçϱíËùÊŸŁșŁšŒÙÉèĂżÁŸł”ŸùÂúÔŰŁ©
ł”ĐÍ | ŒŚ | ÒÒ | ±û |
Æûł”ÔËÔŰÁżŁš¶Ö/ÁŸŁ© | 5 | 8 | 10 |
Æûł”ÔË·ŃŁšÔȘ/ÁŸŁ© | 400 | 500 | 600 |
Łš1Ł©È«ČżÎïŚÊżÉÓĂŒŚĐÍł”8ÁŸŁŹÒÒĐÍł”5ÁŸŁŹ±ûĐÍł” ÁŸÀŽÔËËÍŁź
Łš2Ł©ÈôÈ«ČżÎïŚÊ¶ŒÓĂŒŚĄąÒÒÁœÖÖł”ĐÍÀŽÔËËÍŁŹĐèÔË·Ń8200ÔȘŁŹÎÊ·Ö±đĐèŒŚĄąÒÒÁœÖÖł”ĐÍžśŒžÁŸŁż
Łš3Ł©ÎȘÁËœÚÊĄÔË·ŃŁŹžĂ”ŰŐțžźŽòËăÓĂŒŚĄąÒÒĄą±ûÈęÖÖł”ĐÍÍŹÊ±ČÎÓëÔËËÍŁŹÒŃÖȘËüĂǔČÜÁŸÊęÎȘ14ÁŸŁŹÄăÄÜ·Ö±đÇółöÈęÖÖł”ĐÍ”ÄÁŸÊęÂ𣿎Ëʱ”ÄÔË·ŃÓÖÊǶàÉÙÔȘŁż