题目内容
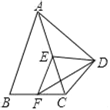
【题目】如图,在△ABC中,AD为BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
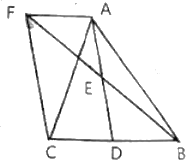
(1)四边形AFCD是什么特殊的四边形?请说明理由.
(2)填空:
①若AB=AC,则四边形AFCD是_______形.
②当△ABC满足条件______时,四边形AFCD是正方形.
【答案】(1)平行四边形,理由见解析; (2)①矩形,②AB=AC,∠BAC=90.
【解析】
(1)由“AAS”可证△AEF≌△DEB,可得AF=BD=CD,由平行四边形的判定可得四边形AFCD是平行四边形;
(2)①由等腰三角形的性质可得AD⊥BC,可证平行四边形AFCD是矩形;
②由等腰直角三角形的性质可得AD=CD=BD,AD⊥BC,可证平行四边形AFCD是正方形.
解:(1)平行四边形
理由如下:∵AF∥BC
∴∠AFE=∠DBE,
在ΔAFE与△DBE中
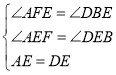
∴ΔAFE≌ΔDBE
∴AF=BD,
又BD=CD
∴AF=CD
又AF∥CD
∴四边形AFCD是平行四边形;
(2)①∵AB=AC,AD是BC边上的中线
∴AD⊥BC,且四边形AFCD是平行四边形
∴四边形AFCD是矩形;
②当△ABC满足AB=AC,∠BAC=90°条件时,四边形AFCD是正方形.
理由为:∵AB=AC,∠BAC=90°,AD是BC边上的中线
∴AD=CD=BD,AD⊥BC
∵四边形AFCD是平行四边形,AD⊥BC
∴四边形AFCD是矩形,且AD=CD
∴四边形AFCD是正方形.
故答案为:(1)平行四边形,理由见解析; (2)①矩形,②AB=AC,∠BAC=90.

练习册系列答案
相关题目